题目内容
已知椭圆C: ,直线l:y=ax+b(a,b∈R)
,直线l:y=ax+b(a,b∈R)
(1)请你给出a,b的一组值,使直线l和椭圆C相交
(2)直线l和椭圆C相交时,a,b应满足什么关系?
(3)若a+b=1,试判断直线l和椭圆C的位置关系;
(4)请你在第(3)问的基础上添加一个合适的条件,求出直线l的方程,
(5)先将试题中的椭圆方程改为双曲线方程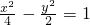 ,或改为抛物线方程y2=4x,再在第(4)问添加的条件中选择一个,求出直线l的方程.
,或改为抛物线方程y2=4x,再在第(4)问添加的条件中选择一个,求出直线l的方程.
解:(1)取a=1,b=0,则直线l:y=x和椭圆C相交;
(2)直线l:y=ax+b代入椭圆C: ,可得(1+2a2)x2+4abx+2b2-4=0
,可得(1+2a2)x2+4abx+2b2-4=0
∵直线l和椭圆C相交,∴△=(4ab)2-4(1+2a2)(2b2-4)>0,∴b2-4a2-2<0
(3)∵a+b=1,∴b=1-a,∴y=ax+1-a,即y-1=a(x-1),∴直线l恒过(1,1)
(1,1)代入椭圆C: ,可得
,可得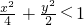 ,所以(1,1)在椭圆内
,所以(1,1)在椭圆内
所以直线l和椭圆C恒相交;
(4)添加条件:直线l过点(2,0),则a=-1,∴直线l的方程为x+y-2=0;
(5)椭圆方程改为双曲线方程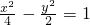 ,或改为抛物线方程y2=4x,添加条件:直线l过点(2,0),则a=-1,∴直线l的方程为x+y-2=0.
,或改为抛物线方程y2=4x,添加条件:直线l过点(2,0),则a=-1,∴直线l的方程为x+y-2=0.
分析:(1)取a=1,b=0,则直线l:y=x和椭圆C相交;
(2)直线l:y=ax+b代入椭圆C: ,利用直线l和椭圆C相交,可得△>0,即可确定a,b应满足的关系;(3)由a+b=1,可得直线l恒过(1,1),进而可得(1,1)在椭圆内,即可判断直线l和椭圆C恒相交;
,利用直线l和椭圆C相交,可得△>0,即可确定a,b应满足的关系;(3)由a+b=1,可得直线l恒过(1,1),进而可得(1,1)在椭圆内,即可判断直线l和椭圆C恒相交;
(4)添加条件:直线l过点(2,0),则a=-1,可求直线l的方程;
(5)椭圆方程改为双曲线方程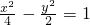 ,或改为抛物线方程y2=4x,添加条件:直线l过点(2,0),可得直线l的方程.
,或改为抛物线方程y2=4x,添加条件:直线l过点(2,0),可得直线l的方程.
点评:本题是开放题,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.
(2)直线l:y=ax+b代入椭圆C:
 ,可得(1+2a2)x2+4abx+2b2-4=0
,可得(1+2a2)x2+4abx+2b2-4=0∵直线l和椭圆C相交,∴△=(4ab)2-4(1+2a2)(2b2-4)>0,∴b2-4a2-2<0
(3)∵a+b=1,∴b=1-a,∴y=ax+1-a,即y-1=a(x-1),∴直线l恒过(1,1)
(1,1)代入椭圆C:
 ,可得
,可得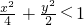 ,所以(1,1)在椭圆内
,所以(1,1)在椭圆内所以直线l和椭圆C恒相交;
(4)添加条件:直线l过点(2,0),则a=-1,∴直线l的方程为x+y-2=0;
(5)椭圆方程改为双曲线方程
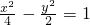 ,或改为抛物线方程y2=4x,添加条件:直线l过点(2,0),则a=-1,∴直线l的方程为x+y-2=0.
,或改为抛物线方程y2=4x,添加条件:直线l过点(2,0),则a=-1,∴直线l的方程为x+y-2=0.分析:(1)取a=1,b=0,则直线l:y=x和椭圆C相交;
(2)直线l:y=ax+b代入椭圆C:
 ,利用直线l和椭圆C相交,可得△>0,即可确定a,b应满足的关系;(3)由a+b=1,可得直线l恒过(1,1),进而可得(1,1)在椭圆内,即可判断直线l和椭圆C恒相交;
,利用直线l和椭圆C相交,可得△>0,即可确定a,b应满足的关系;(3)由a+b=1,可得直线l恒过(1,1),进而可得(1,1)在椭圆内,即可判断直线l和椭圆C恒相交;(4)添加条件:直线l过点(2,0),则a=-1,可求直线l的方程;
(5)椭圆方程改为双曲线方程
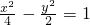 ,或改为抛物线方程y2=4x,添加条件:直线l过点(2,0),可得直线l的方程.
,或改为抛物线方程y2=4x,添加条件:直线l过点(2,0),可得直线l的方程.点评:本题是开放题,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
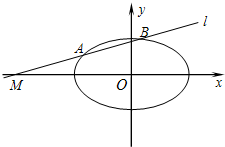 已知椭圆C:
已知椭圆C: ,直线l过点M(m,0).
,直线l过点M(m,0).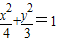 ,直线l过点M(m,0).
,直线l过点M(m,0).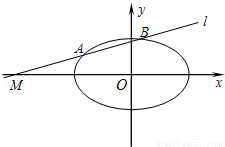
 ,直线l与椭圆C相交于A、B两点,
,直线l与椭圆C相交于A、B两点, (其中O为坐标原点).
(其中O为坐标原点).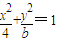 ,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )