题目内容
 已知椭圆C:
已知椭圆C: ,直线l过点M(m,0).
,直线l过点M(m,0).
(Ⅰ)若直线l交y轴于点N,当m=-1时,MN中点恰在椭圆C上,求直线l的方程;
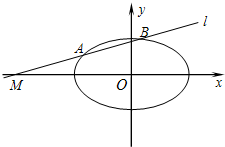
(Ⅱ)如图,若直线l交椭圆C于A,B两点,当m=-4时,在x轴上是否存在点p,使得△PAB为等边三角形?若存在,求出点p坐标;若不存在,请说明理由.
解:(Ⅰ)设点N(0,n),则MN的中点为(- ,
, ),
),
∴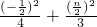 =1,解得n=
=1,解得n=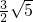 ,
,
所以直线l的方程为:y=±
 (x+1).
(x+1).
(Ⅱ)假设在x轴上存在点P,使得△PAB为等边三角形.
设直线l为x=ty-4,A(x1,y1),B(x2,y2),
则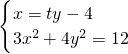 ,∴(3t2+4)y2-24ty+36=0,
,∴(3t2+4)y2-24ty+36=0,
∴y1+y2=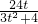 ,
,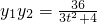 ,△=144(t2-4)>0,
,△=144(t2-4)>0,
∴AB中点为(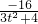 ,
,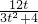 ),
),
∴AB的中垂线为:y-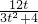 =-t(x+
=-t(x+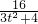 ),
),
∴点P为(-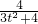 ,0),∴P到直线l的距离d=
,0),∴P到直线l的距离d=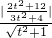 =
=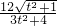 ,
,
∵|AB|=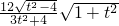 ,
,
∴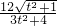 =
=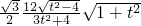 ,
,
∴t=± ,
,
∴存在点P为(- ,0).
,0).
分析:(Ⅰ)设点N(0,n),表示出MN中点坐标,代入椭圆方程即可求得n值,从而可得直线方程;
(Ⅱ)假设在x轴上存在点P,使得△PAB为等边三角形.设直线l为x=ty-4,写出AB中垂线方程,进而得到P点坐标,表示出P到直线l的距离d,据弦长公式求出|AB|,则有d= •|AB|
•|AB|
,解出即可,注意要保证直线与椭圆有两个交点,即直线与椭圆方程联立消元后△>0.
点评:本题考查直线与圆锥曲线的综合问题、直线方程,考查学生的运算变形能力,考查学生分析解决问题的能力.
 ,
, ),
),∴
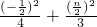 =1,解得n=
=1,解得n=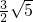 ,
,所以直线l的方程为:y=±

 (x+1).
(x+1). (Ⅱ)假设在x轴上存在点P,使得△PAB为等边三角形.
设直线l为x=ty-4,A(x1,y1),B(x2,y2),
则
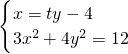 ,∴(3t2+4)y2-24ty+36=0,
,∴(3t2+4)y2-24ty+36=0,∴y1+y2=
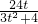 ,
,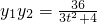 ,△=144(t2-4)>0,
,△=144(t2-4)>0,∴AB中点为(
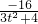 ,
,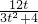 ),
),∴AB的中垂线为:y-
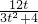 =-t(x+
=-t(x+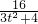 ),
),∴点P为(-
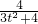 ,0),∴P到直线l的距离d=
,0),∴P到直线l的距离d=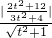 =
=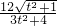 ,
,∵|AB|=
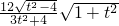 ,
,∴
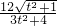 =
=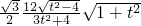 ,
,∴t=±
 ,
,∴存在点P为(-
 ,0).
,0).分析:(Ⅰ)设点N(0,n),表示出MN中点坐标,代入椭圆方程即可求得n值,从而可得直线方程;
(Ⅱ)假设在x轴上存在点P,使得△PAB为等边三角形.设直线l为x=ty-4,写出AB中垂线方程,进而得到P点坐标,表示出P到直线l的距离d,据弦长公式求出|AB|,则有d=
 •|AB|
•|AB|,解出即可,注意要保证直线与椭圆有两个交点,即直线与椭圆方程联立消元后△>0.
点评:本题考查直线与圆锥曲线的综合问题、直线方程,考查学生的运算变形能力,考查学生分析解决问题的能力.

练习册系列答案
相关题目
 ,直线l:y=ax+b(a,b∈R)
,直线l:y=ax+b(a,b∈R)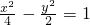 ,或改为抛物线方程y2=4x,再在第(4)问添加的条件中选择一个,求出直线l的方程.
,或改为抛物线方程y2=4x,再在第(4)问添加的条件中选择一个,求出直线l的方程.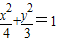 ,直线l过点M(m,0).
,直线l过点M(m,0).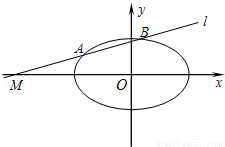
 ,直线l与椭圆C相交于A、B两点,
,直线l与椭圆C相交于A、B两点, (其中O为坐标原点).
(其中O为坐标原点).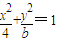 ,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )