题目内容
10．设函数f（x）=x2-log2（2x+2）．若0＜b＜1，则f（b）的值满足（ ）| A． | f（b）＞f（-$\frac{3}{4}$） | B． | f（b）＞0 | C． | f（b）＞f（2） | D． | f（b）＜f（2） |
分析 作出函数y=x2与y=log2（2x+2）的图象，可发现f（b）＜0，计算f（-$\frac{3}{4}$），f（2）的值即可得出答案．
解答 解：作出y=x2与y=log2（2x+2）的图象如图：
由图象可知当0＜x＜1时，x2＜log2（2x+2）．
∵0＜b＜1，∴f（b）=b2-log2（2b+2）＜0，排除B；
∵f（-$\frac{3}{4}$）=$\frac{9}{16}$+1=$\frac{25}{16}$＞0，排除A；
f（2）=4-log26＞0，排除C．
故选：D．
点评 本题考查了函数图象的变换及函数值计算，是基础题．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
20．f（x）=ax2+2（a-1）x+2在（-∞，4]上单调递减，则a的取值范围是（ ）
| A． | $a≤\frac{1}{5}$ | B． | $a≥\frac{1}{5}$ | C． | $0＜a≤\frac{1}{5}$ | D． | $0≤a≤\frac{1}{5}$ |
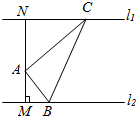如图，A是两条平行直线之间的一定点，且点A到两平行直线的距离分别为AM=1，AN=$\sqrt{2}$，设△ABC，AC⊥AB，且顶点B、C分别在两平行直线上运动，则
2．经过点M（1，1）且在两轴上截距相等的直线是（ ）
| A． | x+y=2 | B． | x+y=1 | C． | x=1或y=1 | D． | x+y=2或x-y=0 |