题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分其中①6分、②2分。
设抛物线
 的焦点为
的焦点为 ,过
,过 且垂直于
且垂直于 轴的直线与抛物线交于
轴的直线与抛物线交于 两点,已知
两点,已知 .
.
(1)求抛物线 的方程;
的方程;
(2)设 ,过点
,过点 作方向向量为
作方向向量为 的直线与抛物线
的直线与抛物线 相交于
相交于 两点,求使
两点,求使 为钝角时实数
为钝角时实数 的取值范围;
的取值范围;
(3)①对给定的定点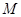
 ,过
,过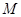 作直线与抛物线
作直线与抛物线 相交于
相交于 两点,问是否存在一条垂直于
两点,问是否存在一条垂直于 轴的直线与以线段
轴的直线与以线段 为直径的圆始终相切?若存在,请求出这条直线;若不存在,请说明理由。
为直径的圆始终相切?若存在,请求出这条直线;若不存在,请说明理由。
②对 ,过
,过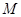 作直线与抛物线
作直线与抛物线 相交于
相交于 两点,问是否存在一条垂直于
两点,问是否存在一条垂直于 轴的直线与以线段
轴的直线与以线段 为直径的圆始终相切?(只要求写出结论,不需用证明)
为直径的圆始终相切?(只要求写出结论,不需用证明)
(1)
(2)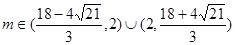
(3)①不存在
②当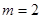 时,存在直线
时,存在直线 满足条件;
满足条件;
当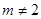 且
且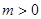 时,直线不存在。
时,直线不存在。
【解析】设、列、解”三部曲是解答数学问题的基本方法,设的巧妙,列的合理,解的准确快速,这是考试的基本要求,也是平时训练的最高追求所在.抛物线的考查仍为热点,平面向量的渗入仍然是大趋势,把向量的表达式能熟练转化为其坐标表达式(特别是用其横坐标分量或是纵坐标分量的表示)显得非常重要;直线与抛物线的位置关系不会抛开二次方程的根与系数的关系,给定参数的范围求某变量的取值范围是高考数学在二次曲线板块的特点,应值得注意。
解:(1)由条件得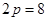 ,
, 抛物线C的方程为
抛物线C的方程为 ;…………………. 4分
;…………………. 4分
(2)直线方程为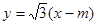 代入
代入 得
得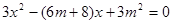 ,
,
设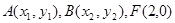 ,则
,则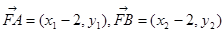 ,
,
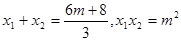 。……………………………. 6分
。……………………………. 6分
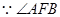 为钝角,
为钝角,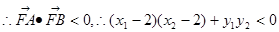 ,即
,即
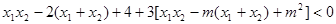 ,
,
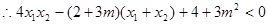 ,……………………………. 8分
,……………………………. 8分
因此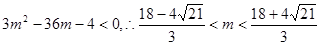 ,………………. 9分
,………………. 9分
综上得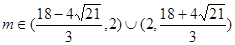 。………………………. 10分
。………………………. 10分
(3)①设过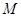 所作直线方程为
所作直线方程为 代入
代入 得
得
 ,…………………………….11 分
,…………………………….11 分
设 则
则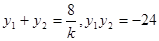 ,
,
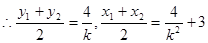 ,
, 中点
中点 ,…………………. 12分
,…………………. 12分
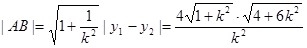 。………………………. 13分
。………………………. 13分
设存在直线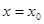 满足条件,则
满足条件,则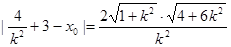 , ……………………………. 14分
, ……………………………. 14分
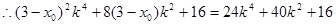 对任意
对任意 恒成立,
恒成立,
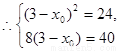 无解,
无解,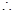 这样的直线不存在。 …………………. 16分
这样的直线不存在。 …………………. 16分
②当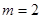 时,存在直线
时,存在直线 满足条件;………………………….17分
满足条件;………………………….17分
当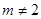 且
且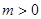 时,直线不存在。 …………………………….18分
时,直线不存在。 …………………………….18分
【解析】

 名校课堂系列答案
名校课堂系列答案 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处