题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）的离心率为 
，以原点为圆心，椭圆的短半轴为半径的圆与直线x﹣y+ 
=0相切，过点P（4，0）且不垂直于x轴直线l与椭圆C相交于A、B两点．
（1）求椭圆C的方程；
（2）求 
的取值范围；
（3）若B点关于x轴的对称点是E，证明：直线AE与x轴相交于定点．
【答案】
（1）解：由题意知， 
， 
即b= 
又a2=b2+c2
∴a=2，b=
故椭圆的方程为 
（2）解：由题意知直线l的斜率存在，设直线l的方程为y=k（x﹣4）
由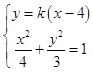 
可得：（3+4k2）x2﹣32k2x+64k2﹣12=0
设A（x1，y1），B （x2，y2），则△=322k4﹣4（3+4k2）（64k2﹣12）＞0
∴ 
∴x1+x2= 
，x1x2= 
①
∴ 
=x1x2+y1y2= 
= 
= 
= 
∵
∴ 
∴ 
∴ 
（3）证明：∵B，E关于x轴对称
∴可设E（x2，﹣y2）
∴直线AE的方程为 
令y=0可得x= 
∵y1=k（x1﹣4），y2=k（x2﹣4）
∴ 
= 
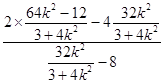=1
∴直线AE与x轴交于定点（1，0）
【解析】（1）由题意知， ，利用点到直线的距离公式可求b，结合a2=b2+c2可求a，即可求解（2）由题意设直线l的方程为y=k（x﹣4），联立直线与椭圆方程，设A（x1 ， y1），B （x2 ， y2），根据方程的根与系数关系求出x1+x2 ， x1x2 ， 由△＞0可求k的范围，然后代入 =x1x2+y1y2= = 中即可得关于k的方程，结合k的范围可求 的范围（3）由B，E关于x轴对称可得E（x2 ， ﹣y2），写出AE的方程，令y=0，结合（2）可求
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
．
