题目内容
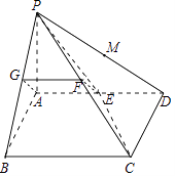
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2, ![]() ,E、F分别为AD、PC中点.
,E、F分别为AD、PC中点. 
(1)求点F到平面PAB的距离;
(2)求证:平面PCE⊥平面PBC;
(3)求二面角E﹣PC﹣D的大小.
【答案】
(1)解:如图,取PB中点G,连接FG、AG,
∵底面ABCD为菱形,且PA=AD=2,BD= ![]() ,∴底面ABCD为正方形,
,∴底面ABCD为正方形,
∵E、F分别为AD、PC中点,∴FG∥BC,FG= ![]() ,AE∥BC,AE=
,AE∥BC,AE= ![]() ,
,
则FG∥AE且FG=AE,四边形AEFG为平行四边形,故AG∥FE,
∵AG平面PAB,EF平面PAB,∴EF∥平面PAB,
∴点F与点E到平面PAB的距离相等,即距离为EA=1
(2)证明:由(1)知,AG⊥PB,AG∥EF,
∵PA⊥平面ABCD,∴BC⊥PA,
∵BC⊥AB,AB∩BC=B,∴BC⊥平面PAB,
∴BC⊥AG,又PB∩BC=B,
∴AG⊥平面PBC,则EF⊥平面PBC,
∵EF平面PCE,∴平面PCE⊥平面PBC
(3)解:作EM⊥PD于M,连接FM,
∵CD⊥平面PAD,∴CD⊥EM,
∴EM⊥平面PCD,则EM⊥PC.
由(2)知,EF⊥平面PBC,∴EF⊥PC,
又EM∩EF=E,∴PC⊥平面EFM,
∴FM⊥PC,
∴∠MFE为二面角E﹣PC﹣D的平面角或其补角.
∵PA=AD=2,∴EF=AG= ![]() ,EM=
,EM= ![]() .
.
∴sin∠MEF= ![]() ,则∠MFE=30°.
,则∠MFE=30°.
即二面角E﹣PC﹣D的大小为30°.

【解析】(1)取PB中点G,连接FG、AG,由已知可得底面ABCD为正方形,再由E、F分别为AD、PC中点,可得四边形AEFG为平行四边形,得到AG∥FE,由线面平行的判定可得EF∥平面PAB,从而得到点F与点E到平面PAB的距离相等,即距离为EA=1;(2)由(1)知,AG⊥PB,AG∥EF,再由PA⊥平面ABCD,可得BC⊥PA,由线面垂直的判定可得BC⊥平面PAB,得到BC⊥AG,进一步得到AG⊥平面PBC,则EF⊥平面PBC,由面面垂直的判定可得平面PCE⊥平面PBC;(3)作EM⊥PD于M,连接FM,由CD⊥平面PAD,得CD⊥EM,进一步得到EM⊥PC.结合(2)知,EF⊥平面PBC,即EF⊥PC,可得FM⊥PC,从而得到∠MFE为二面角E﹣PC﹣D的平面角或其补角.然后求解三角形可得二面角E﹣PC﹣D的大小为30°.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直.

【题目】某车间为了给贫困山区的孩子们赶制一批爱心电子产品,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下表所示:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 |
| 3 | 4 |
|
经统计发现零件个数![]() 与加工时间
与加工时间![]() 具有线性相关关系.
具有线性相关关系.
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)试预测加工10个零件需要多少时间.
利用公式: ,
,![]()
【题目】种植于道路两侧、为车辆和行人遮阴并构成街景的乔木称为行道树![]() 为确保行人、车辆和临近道路附属设施安全,树木与原有电力线之间的距离不能超出安全距离
为确保行人、车辆和临近道路附属设施安全,树木与原有电力线之间的距离不能超出安全距离![]() 按照北京市
按照北京市![]() 行道树修剪规范
行道树修剪规范![]() 要求,当树木与原有电力线发生矛盾时,应及时修剪树枝
要求,当树木与原有电力线发生矛盾时,应及时修剪树枝![]() 行道树修剪规范
行道树修剪规范![]() 中规定,树木与原有电力线的安全距离如表所示:树木与电力线的安全距离表
中规定,树木与原有电力线的安全距离如表所示:树木与电力线的安全距离表
电力线 | 安全距离 | |
水平距离 | 垂直距离 | |
|
|
|
|
|
|
|
|
|
|
|
|
330KV |
|
|
500KV |
|
|
现有某棵行道树已经自然生长2年,高度为![]() 据研究,这种行道树自然生长的时间
据研究,这种行道树自然生长的时间![]() 年
年![]() 与它的高度
与它的高度![]() 满足关系式
满足关系式![]()
![]() 1
1![]() ______;
______;![]() 将结果直接填写在答题卡的相应位置上
将结果直接填写在答题卡的相应位置上![]()
![]() 2
2![]() 如果这棵行道树的正上方有35kV的电力线,该电力线距地面
如果这棵行道树的正上方有35kV的电力线,该电力线距地面![]() 那么这棵行道树自然生长多少年必须修剪?
那么这棵行道树自然生长多少年必须修剪?
![]() 3
3![]() 假如这棵行道树的正上方有500KV的电力线,这棵行道树一直自然生长,始终不会影响电力线段安全,那么该电力线距离地面至少多少米?
假如这棵行道树的正上方有500KV的电力线,这棵行道树一直自然生长,始终不会影响电力线段安全,那么该电力线距离地面至少多少米?
