题目内容
已知a、b、c∈R+,a、b、c互不相等且abc=1.求证: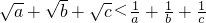 .
.
(本小题满分14分)
证明:∵a、b、c∈R+且互不相等,且abc=1
∴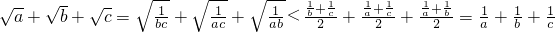 .
.
故不等式成立.
分析:根据条件可化为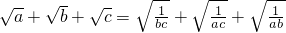 ,应用基本不等式即可证得结论.
,应用基本不等式即可证得结论.
点评:本题考查基本不等式,难点在于对条件的合理转化即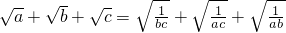 的转化,属于中档题.
的转化,属于中档题.
证明:∵a、b、c∈R+且互不相等,且abc=1
∴
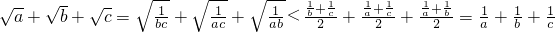 .
.故不等式成立.
分析:根据条件可化为
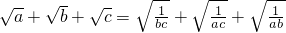 ,应用基本不等式即可证得结论.
,应用基本不等式即可证得结论.点评:本题考查基本不等式,难点在于对条件的合理转化即
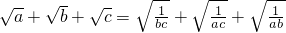 的转化,属于中档题.
的转化,属于中档题. 
练习册系列答案
相关题目