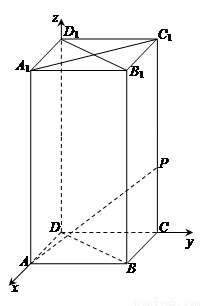题目内容
如图,棱长为1的正四面体ABCD中,E、F分别是棱AD、CD的中点,O是点A在平面BCD内的射影.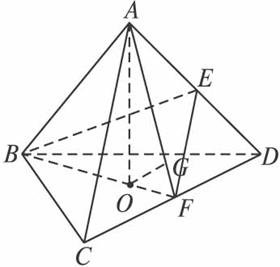
(1)求直线EF与直线BC所成角的大小;
(2)求点O到平面ACD的距离;
(3)(理)求二面角ABEF的大小.
(文)求二面角CBFE的大小.
解:方法一:(1)因为E、F分别是棱AD、CD的中点,所以EF∥AC.所以∠BCA是EF与BC所成角.因为正四面体ABCD,所以△ABC为正三角形.所以∠BCA=60°,即EF与BC所成角的大小是60°.
(2)解法一:如图,连结AO,AF,

因为F是CD的中点,且△ACD,△BCD均为正三角形,所以BF⊥CD,AF⊥CD.因为BF∩AF=F,所以CD⊥面AFB.因为CD![]() 面ACD,所以面AFB⊥面ACD.因为ABCD是正四面体,且O是点A在面BCD内的射影,所以点O必在正三角形BCD的中线BF上.在面ABF中,过O作OG⊥AF,垂足为G,所以OG⊥面ACD,即OG的长为点O到面ACD的距离.因为正四面体ABCD的棱长为1,在△ABF中,容易求出AF=BF=
面ACD,所以面AFB⊥面ACD.因为ABCD是正四面体,且O是点A在面BCD内的射影,所以点O必在正三角形BCD的中线BF上.在面ABF中,过O作OG⊥AF,垂足为G,所以OG⊥面ACD,即OG的长为点O到面ACD的距离.因为正四面体ABCD的棱长为1,在△ABF中,容易求出AF=BF=![]() ,OF=
,OF=![]() ,AO=
,AO=![]() ,因为△AOF∽△OGF,故由相似比易求出OG=
,因为△AOF∽△OGF,故由相似比易求出OG=![]() .所以点O到平面ACD的距离是
.所以点O到平面ACD的距离是![]() .
.
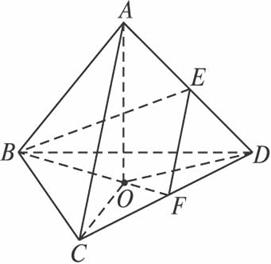
解法二:如图,连结AO,CO,DO,所以点O到平面ACD的距离就是三棱锥O—ACD底面ACD上的高h.与解法一同理容易求出OF=![]() ,AO=
,AO=![]() ,所以VA—COD=
,所以VA—COD=![]() ·
·![]() (
(![]() ·
·![]() ·1)=
·1)=![]() .
.
因为VO—ACD=VA—COD,所以![]() =VO—ACD=
=VO—ACD=![]() ·h·(
·h·(![]() ·
·![]() ·1).解得h=
·1).解得h=![]() .
.
(3)(理)设△ABD中,AB边的中线交BE于H,连结CH,则由ABCD为正四面体知CH⊥面ABD.
设HD的中点为K,则FK∥CH.
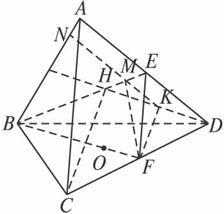
所以FK⊥面ABD.在面ABD内,过点K作KN∥AD,KN交BE于M,交AB于N,因为BE⊥AD,所以NM⊥BE.连结FM,所以FM⊥BE.所以∠NMF是所求二面角的平面角.
因为FK=![]() CH=
CH=![]() ·
·![]() =
=![]() ,MK=
,MK=![]() ED=
ED=![]() AD=
AD=![]() ,所以tan∠FMK=
,所以tan∠FMK=![]() =
=![]() .
.
所以tan∠NMF=tan(π-∠FMK)=![]() .所以所求二面角的大小为π-arctan
.所以所求二面角的大小为π-arctan![]() .
.
(或者由正四面体的对称性,可转求二面角CBFE的大小)
(文)连结OD,设OD的中点为K,连结EK,
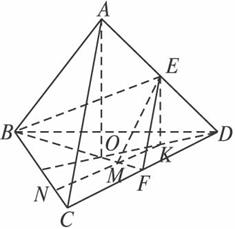
则EK∥AO.因为AO⊥面BCD,所以EK⊥面BCD.在平面BCD内,过点K作KN∥CD,KN交BF于M,交BC于N,因为BF⊥CD,所以KN⊥BF.连结EM,所以EM⊥BF.所以∠NME是所求二面角的平面角.
因为EK=![]() AO=
AO=![]() ·
·![]() =
=![]() ,MK=
,MK=![]() FD=
FD=![]() CD=
CD=![]() ,所以tan∠EMK=
,所以tan∠EMK=![]() =
=![]() .
.
所以tan∠NME=tan(π-∠EMK)=![]() .所以所求二面角的大小为π-arctan
.所以所求二面角的大小为π-arctan![]() .
.
方法二:如图,以点A在面BCD的射影O为坐标原点,有向直线OA为z轴,有向直线BF为y轴,x轴为过点O与DC平行的有向直线.
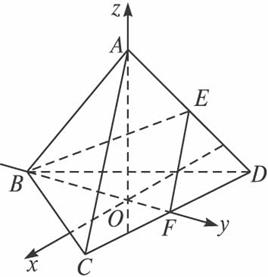
因为正四面体ABCD的棱长为1,
所以可以求出各点的坐标依次为:O(0,0,0),A(0,0,![]() ),B(0,-
),B(0,-![]() ,0),C(
,0),C(![]() ,
,![]() ,0),D(-
,0),D(-![]() ,
,![]()
,0),E(-![]() ,
,![]() ,
,![]() ),F(0,
),F(0,![]() ,0).
,0).
(1)因为![]() =(
=(![]() ,
,![]() ,-
,-![]() ),
),![]() =(
=(![]() ,
,![]() ,0),又
,0),又![]() =
=![]() ×
×![]() +
+![]() ×
×![]() -
-![]() ×0
×0
=![]() +
+![]() =
=![]() ,且|
,且|![]() |=
|=![]() |
|![]() |=
|=![]() ,|
,|![]() |=1,所以cos〈
|=1,所以cos〈![]() 〉=
〉=![]() =
=![]() .
.
所以EF与BC所成角的大小是60°.
(2)因为![]() =(
=(![]() ,
,![]() ,-
,-![]() ),
),![]() =(-
=(-![]() ,
,![]() ,-
,-![]() ),
),
设平面ACD的一个法向量为FACD=(x1,y1,z1),由![]() ·FACD=0,
·FACD=0,![]() ·FACD=0,
·FACD=0,
解得FACD=(0,2,![]() ).因为
).因为![]() =(0,
=(0,![]() ,0),
,0),![]() ·FACD=
·FACD=![]() ,|FACD|=
,|FACD|=![]() ,
,
所以点O到平面ACD的距离d=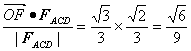 .
.
(3)(理)因为![]() =(0,-
=(0,-![]() ,-
,-![]() ),
),![]() =(-
=(-![]() ,
,![]() ,-
,-![]() ),
),
设平面ABD的一个法向量为FABD=(x2,y2,z2),由![]() ·FABD=0,
·FABD=0,![]() ·FABD=0,
·FABD=0,
可得一个法向量FABD=(![]() ).
).
同理可以求出平面BEF的一个法向量为FBEF=(![]() ,0,3).
,0,3).
因为FABD·FBEF=-9,|FABD|=3,|FBEF|=![]() ,所以cosβ=
,所以cosβ=![]() .
.
所以二面角ABEF的大小为arccos(![]() )=π-arccos
)=π-arccos![]() .
.
(文)因为![]() =(
=(![]() ,
,![]() ,-
,-![]() ),
),![]() =(0,
=(0,![]() ,0),设平面BEF的一个法向量为FBEF=(x2,y2,z2),
,0),设平面BEF的一个法向量为FBEF=(x2,y2,z2),
由![]() ·FBEF=0,
·FBEF=0,![]() ·FBEF=0,可得平面BEF的一个法向量FBEF=(
·FBEF=0,可得平面BEF的一个法向量FBEF=(![]() ,0,3).
,0,3).
容易得到平面BCF的一个法向量FBCF=(0,0,-1).因为FBEF·FBCF=-3,|FBEF|=![]() ,|FBCF|=1,
,|FBCF|=1,
所以cosβ=![]() .
.
所以二面角CBFE的大小为arccos(![]() )=π-arccos
)=π-arccos![]() .
.

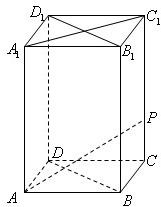 如图,在底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.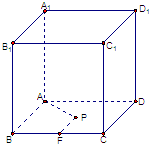 如图:在底面边长为1的正四棱柱ABCD-A1B1C1D1中,P为底面ABCD所在平面内一动点,点P到直线BC的距离等于它到直线AA1的距离,则P点的轨迹方程是( )
如图:在底面边长为1的正四棱柱ABCD-A1B1C1D1中,P为底面ABCD所在平面内一动点,点P到直线BC的距离等于它到直线AA1的距离,则P点的轨迹方程是( ) (2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,
(2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱, (2009•闵行区二模)(文)如图几何体是由一个棱长为2的正方体ABCD-A1B1C1D1与一个侧棱长为2的正四棱锥P-A1B1C1D1组合而成.
(2009•闵行区二模)(文)如图几何体是由一个棱长为2的正方体ABCD-A1B1C1D1与一个侧棱长为2的正四棱锥P-A1B1C1D1组合而成.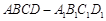 中,P是侧棱
中,P是侧棱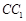 上的一点,
上的一点,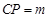 . (1)试确定m,使直线AP与平面BDD1B1所成角为60º;(2)在线段
. (1)试确定m,使直线AP与平面BDD1B1所成角为60º;(2)在线段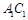 上是否存在一个定点
上是否存在一个定点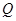 ,使得对任意的m,
,使得对任意的m,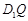 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论.