题目内容
 (2009•闵行区二模)(文)如图几何体是由一个棱长为2的正方体ABCD-A1B1C1D1与一个侧棱长为2的正四棱锥P-A1B1C1D1组合而成.
(2009•闵行区二模)(文)如图几何体是由一个棱长为2的正方体ABCD-A1B1C1D1与一个侧棱长为2的正四棱锥P-A1B1C1D1组合而成.(1)求该几何体的主视图的面积;
(2)若点E是棱BC的中点,求异面直线AE与PA1所成角的大小(结果用反三角函数表示).
分析:(1)画出其主视图,可知其面积S为三角形与正方形面积之和,求出在正四棱锥P-A1B1C1D1中棱锥的高,即可求出该几何体的主视图的面积;
(2)取B1C1中点E1,连接A1E1则∠PA1E1为异面直线AE与PA1所成角,然后利用余弦定理求出此角的余弦值,最后利用反三角表示出此角即可.
(2)取B1C1中点E1,连接A1E1则∠PA1E1为异面直线AE与PA1所成角,然后利用余弦定理求出此角的余弦值,最后利用反三角表示出此角即可.
解答: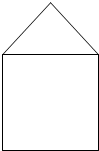 (文)解:(1)画出其主视图(如图),
(文)解:(1)画出其主视图(如图),
可知其面积S为三角形与正方形面积之和.
在正四棱锥P-A1B1C1D1中,棱锥的高h=
,(2分)
S=
•2•
+4=
+4.(6分)
(2)取B1C1中点E1,连接A1E1,∵A1E1∥AE
则∠PA1E1为异面直线AE与PA1所成角.(2分)
在△PA1E1中,A1E1=
,PA1=2,
又在正四棱锥P-A1B1C1D1中,斜高为PE1=
,(4分)
由余弦定理可得 cos∠PA1E1=
=
(6分)
所以∠PA1E1=arccos
,异面直线AE与PA1所成的角为arccos
.(8分)
 (文)解:(1)画出其主视图(如图),
(文)解:(1)画出其主视图(如图),可知其面积S为三角形与正方形面积之和.
在正四棱锥P-A1B1C1D1中,棱锥的高h=
| 2 |
S=
| 1 |
| 2 |
| 2 |
| 2 |
(2)取B1C1中点E1,连接A1E1,∵A1E1∥AE
则∠PA1E1为异面直线AE与PA1所成角.(2分)
在△PA1E1中,A1E1=
| 5 |
又在正四棱锥P-A1B1C1D1中,斜高为PE1=
| 3 |
由余弦定理可得 cos∠PA1E1=
| 4+5-3 | ||
2•2•
|
| 3 |
| 10 |
| 5 |
所以∠PA1E1=arccos
| 3 |
| 10 |
| 5 |
| 3 |
| 10 |
| 5 |
点评:本题主要考查了三视图和异面直线所成角,以及平面图象的面积的计算,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目