题目内容
(1)求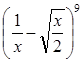 的展开式中的常数项;
的展开式中的常数项;
(2)已知 ,
,
求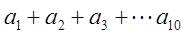 的值.
的值.
(1) ;(2)
;(2)
解析试题分析:(1)由二项式定理的通项展开式公式可得 .故要求所求的常数项即
.故要求所求的常数项即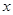 的系数为零即可求得相应的r的值.从而可得常数项.
的系数为零即可求得相应的r的值.从而可得常数项.
(2)由已知 以及结合要得到的结论
以及结合要得到的结论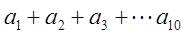 可以设想所有含
可以设想所有含 的部分为1即可令
的部分为1即可令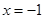 .可是又多了一个
.可是又多了一个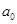 的值,所以要想办法将含有
的值,所以要想办法将含有 部分转化为零即可,所以令
部分转化为零即可,所以令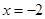 即可得到
即可得到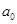 的值从而可得所求的结论.
的值从而可得所求的结论.
试题解析:(1)展开式通项为 .由
.由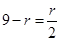 ,可得
,可得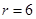 .因此展开式的常数项为第7项:
.因此展开式的常数项为第7项: =
=  .
.
(2)恒等式中赋值,分别令x=-2与x=-1,得到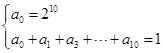 然后两式相减得到
然后两式相减得到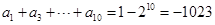 .
.
考点:1.二项式定理的展开式.2.展开式两边的变化对比.3.特殊数字的设定.

练习册系列答案
相关题目
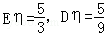 ,求a:b:c.
,求a:b:c. +
+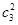 +
+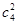 +…+
+…+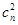 =
=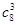 (nεN)
(nεN)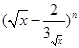 的一次项
的一次项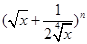 的展开式前三项中的
的展开式前三项中的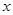 的系数成等差数列.
的系数成等差数列.