题目内容
(本小题满分13分)
已知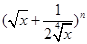 的展开式前三项中的
的展开式前三项中的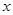 的系数成等差数列.
的系数成等差数列.
(1)求展开式里所有的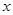 的有理项;
的有理项;
(2)求展开式里系数最大的项.
(1)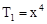 ,
,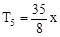 ,
,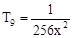 (2)
(2)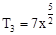 和
和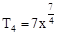
解析试题分析:解:(1)∵ 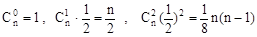
由题设可知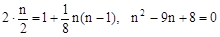 ……………2分
……………2分
解得n=8或n=1(舍去)
当n=8时,通项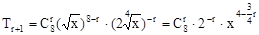 ……………4分
……………4分
据题意,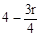 必为整数,从而可知r必为4的倍数,而0≤r≤8
必为整数,从而可知r必为4的倍数,而0≤r≤8
∴ r=0,4,8,故x的有理项为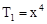 ,
,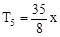 ,
,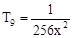 ………6分
………6分
(2)设第r+1项的系数tr+1最大,显然tr+1>0,故有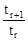 ≥1且
≥1且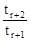 ≤1
≤1
∵ 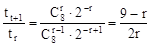 , 由
, 由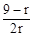 ≥1得r≤3 ……………9分
≥1得r≤3 ……………9分
又∵ 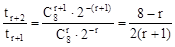 ,由
,由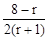 ≤1得:r≥2 ……………11分
≤1得:r≥2 ……………11分
∴ r=2或r=3所求项为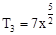 和
和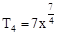 ……………13分
……………13分
考点:等差数列;两项式定理;
点评:两项式定理经常作为考点。在两项式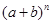 的展开式中,第
的展开式中,第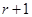 项是
项是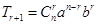 。
。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
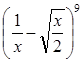 的展开式中的常数项;
的展开式中的常数项; ,
,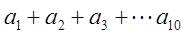 的值.
的值.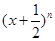 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列. 的值;(2)设
的值;(2)设 .
.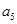 的值; ②求
的值; ②求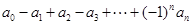 的值.
的值.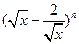 二项展开式中,第4项的二项式系数与第3项的二项式系数的比为
二项展开式中,第4项的二项式系数与第3项的二项式系数的比为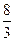 .
.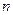 的值;
的值;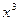 项的系数。
项的系数。
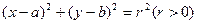 ,从0,3,4,5,6,7,8,9,10这九个数中选出3个不同的数,分别作圆心的横坐标、纵坐标和圆的半径。问:
,从0,3,4,5,6,7,8,9,10这九个数中选出3个不同的数,分别作圆心的横坐标、纵坐标和圆的半径。问: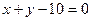 的圆有多少个?
的圆有多少个?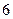 个人坐在一排
个人坐在一排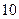 个座位上,问①空位不相邻的坐法有多少种?②
个座位上,问①空位不相邻的坐法有多少种?② 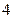 个空位只有
个空位只有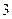 个相邻的坐法有多少种
个相邻的坐法有多少种 ?
?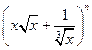 的展开式奇数项的二项式系数之和为
的展开式奇数项的二项式系数之和为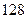 ,则求展开式中二项式系数最大项。
,则求展开式中二项式系数最大项。 件不同的产品排成一排,若其中
件不同的产品排成一排,若其中 ,
, 两件产品排在一起的不同排法有48种,则
两件产品排在一起的不同排法有48种,则