题目内容
现有5名男生和3名女生．
(1)若3名女生必须相邻排在一起，则这8人站成一排，共有多少种不同的排法?
(2)若从中选5人,且要求女生只有2名, 站成一排，共有多少种不同的排法?
(1)4320 (2)3600
解析试题分析：(1) 3名女生必须相邻排在一起,共有不同排法为:
N1＝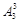
·
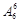＝6×720＝4320； 5分
(2) 从中选5人,且要求女生只有2名, 站成一排，共有不同的排法:
N2＝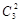
·
·
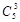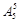＝3600 10分
考点：排列组合
点评：第一问排列时相邻元素采用捆绑法，暂时看做一个元素考虑，第二问采用先选后排的思路结合分步计数原理求解
练习册系列答案
名校课堂系列答案
相关题目
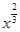＋3x2)n的展开式中，各项系数和比它的二项式系数和大992，求：
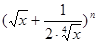的展开式前三项中的
的系数成等差数列.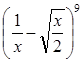
的展开式中的常数项；
，
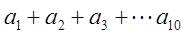的值.
，求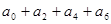
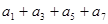的值。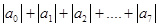
的值。
的值。
的展开式的二项式系数和比
的展开式的系数和大992,求
的展开式中:①二项式系数最大的项;②系数的绝对值最大的项。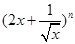
的展开式前两项的二项式系数的和为10.
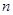的值.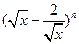 
二项展开式中，第4项的二项式系数与第3项的二项式系数的比为
.
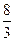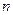的值；
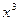项的系数。