题目内容
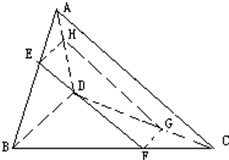 如图,要在呈空间四边形的支架上安装一块矩形的太阳能吸光板(图中EFGH),矩形的四个顶点分别在空间四边形ABCD的边上.已知AC=a,BD=b,试问:E、F、G、H分别在什么位置时,吸光板的面积最大?
如图,要在呈空间四边形的支架上安装一块矩形的太阳能吸光板(图中EFGH),矩形的四个顶点分别在空间四边形ABCD的边上.已知AC=a,BD=b,试问:E、F、G、H分别在什么位置时,吸光板的面积最大?分析:设
=x,则
=1-x,0<x<1,根据矩形EFGH的面积为 EH•EF=x(1-x)ab,可得当x=
时,矩形EFGH的面积最大,此时矩形吸光板的吸光量最大,从而得出结论.
| AE |
| AB |
| BE |
| AB |
| 1 |
| 2 |
解答:解:由题意可得 EH∥FG∥BD,EF∥GH∥AC,
∵AC=a,BD=b,设
=x,则
=1-x,0<x<1,
由三角形相似可得 EH=x•BD,EF=(1-x)•AC,
故矩形EFGH的面积为 EH•EF=x(1-x)ab,
∴当x=
时,矩形EFGH的面积最大,此时矩形吸光板的吸光量最大,
故E、F、G、H在三棱锥的对应边的中点位置时,矩形吸光板的吸光量最大.
∵AC=a,BD=b,设
| AE |
| AB |
| BE |
| AB |
由三角形相似可得 EH=x•BD,EF=(1-x)•AC,
故矩形EFGH的面积为 EH•EF=x(1-x)ab,
∴当x=
| 1 |
| 2 |
故E、F、G、H在三棱锥的对应边的中点位置时,矩形吸光板的吸光量最大.
点评:本题给出平行于四面体相对棱的截面,判定截面的形状并且求截面面积的最大值,着重考查了线面平行性质定理、平行线分线段成比例定理和二次函数的最值等知识,体现了转化的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 8、
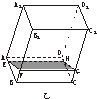
8、 如图甲,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个命题:
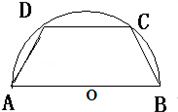
如图甲,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个命题: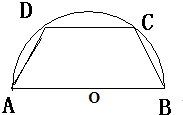 如图,要在半径是2km的半圆形公园内建一个等腰梯形的活动场地,求活动场地的最大面积.
如图,要在半径是2km的半圆形公园内建一个等腰梯形的活动场地,求活动场地的最大面积.