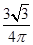题目内容
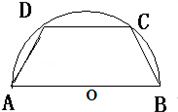
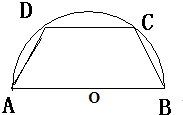 如图,要在半径是2km的半圆形公园内建一个等腰梯形的活动场地,求活动场地的最大面积.
如图,要在半径是2km的半圆形公园内建一个等腰梯形的活动场地,求活动场地的最大面积.分析:设圆心为O,∠BOC=θ,求出四边形的面积表达式,通过导数求出函数的最大值.
解答:解:设圆心为O,∠BOC=θ,
则有S四边形ABCD=
×2×2×sinθ×2+
×2×2×sin(π-2θ)
=4(sinθ+sinθcosθ)(0<θ<
).(6分)
令y=sinθ+sinθcosθ,则y′=2cos2θ+cosθ-1(8分)
若y′=0,则cosθ=
,θ=
,当θ∈(0,
),y/>0,
当θ∈(
,
),y/<0,(11分)
所以当θ=
时,y取极大值也是最大值为3
(km2)(13分).
则有S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
=4(sinθ+sinθcosθ)(0<θ<
| π |
| 2 |
令y=sinθ+sinθcosθ,则y′=2cos2θ+cosθ-1(8分)
若y′=0,则cosθ=
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
当θ∈(
| π |
| 3 |
| π |
| 2 |
所以当θ=
| π |
| 3 |
| 3 |
点评:本题考查三角函数的最值的应用,导数求解函数的最值的求法,考查转化思想计算能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
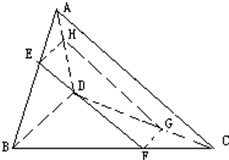 如图,要在呈空间四边形的支架上安装一块矩形的太阳能吸光板(图中EFGH),矩形的四个顶点分别在空间四边形ABCD的边上.已知AC=a,BD=b,试问:E、F、G、H分别在什么位置时,吸光板的面积最大?
如图,要在呈空间四边形的支架上安装一块矩形的太阳能吸光板(图中EFGH),矩形的四个顶点分别在空间四边形ABCD的边上.已知AC=a,BD=b,试问:E、F、G、H分别在什么位置时,吸光板的面积最大? 如图,质点
如图,质点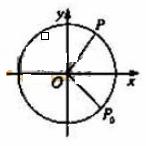

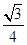 B.
B.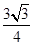 C.
C.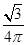 D.
D.