题目内容
(2013•蓟县二模)已知函数f(x)=-
x3+
(2a+1)x2-2ax+1,其中a为实数.
(Ⅰ)当a≠
时,求函数f(x)的极大值点和极小值点;
(Ⅱ) 若对任意a∈(2,3)及x∈[1,3]时,恒有ta2-f(x)>
成立,求实数t的取值范围.
(Ⅲ)已知g(x)=a2x2+ax+1,m(x)=
x3-(a2+
)x2+(2a+5)x-3,h(x)=f(x)+m(x),设函数q(x)=
是否存在a,对任意给定的非零实数x1,存在惟一的非零实数x2(x2≠x1),使得q′(x2)=q′(x1)成立?若存在,求a的值;若不存,请说明理由.
| 1 |
| 3 |
| 1 |
| 2 |
(Ⅰ)当a≠
| 1 |
| 2 |
(Ⅱ) 若对任意a∈(2,3)及x∈[1,3]时,恒有ta2-f(x)>
| 3 |
| 2 |
(Ⅲ)已知g(x)=a2x2+ax+1,m(x)=
| 4 |
| 3 |
| 3 |
| 2 |
|
分析:(Ⅰ)由 f′(x)=-x2+(2a+1)x-2a=0,得x1=1,x2=2a,按两根1与2a的大小关系进行分类讨论,列出f′(x)、f(x)随x的变化情况表,根据极值点的定义可求;
(II)由题意可知,先使得对任意x∈[1,3]时,恒有ta2-f(x)>
成立,然后再使得任意a∈(2,3)时不等式恒成立,分别转化函数最值求解即可;
(Ⅲ)求出x<0和x>0时q′(x)及其值域,易知a≠0,分x1>0和x1<0两种情况进行讨论,按照值域的包含关系可得a的范围;
(II)由题意可知,先使得对任意x∈[1,3]时,恒有ta2-f(x)>
| 3 |
| 2 |
(Ⅲ)求出x<0和x>0时q′(x)及其值域,易知a≠0,分x1>0和x1<0两种情况进行讨论,按照值域的包含关系可得a的范围;
解答:解:(Ⅰ)令 f′(x)=-x2+(2a+1)x-2a=0,解得x1=1,x2=2a,
(1)当a>
时,
因此,函数f(x)在x=1处取得极小值,极小值点为x=1;
函数f(x)在x=2a处取得极大值,极大值点为x=2a;
(2)当a<
时,
因此,函数f(x)在x=1处取得极大值,极大值点为x=1;
函数f(x)在x=2a处取得极小值,极小值点为x=2a.
(II)由题意可知,对任意a∈(2,3)及x∈[1,3]时,恒有ta2-f(x)>
成立等价于ta2-
>f(x)max,
f(x)在x∈[1,3]上的最大值为f(3)=3a-
,
任意a∈(2,3)时,ta2-
>f(x)max=3a-
恒成立,
∴t>
-
,a∈(2,3)时恒成立,
令g(a)=
-
,令m=
,m∈(
,
),g(m)在m∈(
-
)时为增函数,
∴
<g(x)<1,
∴实数t的取值范围为t≥1;
(III)当x<0时,有q′(x)=h′(x)=3x2-2(a2-a-1)x+5,
当x>0时,有q′(x)=g(x)=2a2x+a,因为a=0时不符合题意,因此a≠0,
下面讨论a≠0的情形,记A=(a,+∞),B=(5,+∞),
(i)当x1>0时,q′(x)在(0,+∞)上单调递增,
所以要使q′(x2)=q′(x1)成立,只能x′2<0成立且A⊆B,
因此有a≥5;
(ii)当x1<0时,q′(x)在(-∞,0)上单调递减,
所以要使q′(x2)=q′(x1)成立,只能x2>0且B⊆A,因此a≤5,
综合(i)(ii)a=5;
当a=5时A=B,则?x1<0,q′(x1)∈B=A,即?x2>0,使得q′(x2)=q′(x1)成立,
因为q′(x)在(0,+∞)上单调递增,所以x2的值是唯一的;
同理,?x1>0,即存在唯一的非零实数x2(x2≠x1),q′(x)在(0,+∞)上单调递增,
要使q′(x2)=q′(x1)成立,所以a=5满足题意.
(1)当a>
| 1 |
| 2 |
| x | (-∞,1) | 1 | (1,2a) | 2a | (2a,+∞) |
| f'(x) | - | 0 | + | 0 | - |
函数f(x)在x=2a处取得极大值,极大值点为x=2a;
(2)当a<
| 1 |
| 2 |
| x | (-∞,2a) | 2a | (2a,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + | 0 | - |
函数f(x)在x=2a处取得极小值,极小值点为x=2a.
(II)由题意可知,对任意a∈(2,3)及x∈[1,3]时,恒有ta2-f(x)>
| 3 |
| 2 |
| 3 |
| 2 |
f(x)在x∈[1,3]上的最大值为f(3)=3a-
| 7 |
| 2 |
任意a∈(2,3)时,ta2-
| 3 |
| 2 |
| 7 |
| 2 |
∴t>
| 3 |
| a |
| 2 |
| a2 |
令g(a)=
| 3 |
| a |
| 2 |
| a2 |
| 1 |
| a |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| a |
| 2 |
| a2 |
∴
| 7 |
| 9 |
∴实数t的取值范围为t≥1;
(III)当x<0时,有q′(x)=h′(x)=3x2-2(a2-a-1)x+5,
当x>0时,有q′(x)=g(x)=2a2x+a,因为a=0时不符合题意,因此a≠0,
下面讨论a≠0的情形,记A=(a,+∞),B=(5,+∞),
(i)当x1>0时,q′(x)在(0,+∞)上单调递增,
所以要使q′(x2)=q′(x1)成立,只能x′2<0成立且A⊆B,
因此有a≥5;
(ii)当x1<0时,q′(x)在(-∞,0)上单调递减,
所以要使q′(x2)=q′(x1)成立,只能x2>0且B⊆A,因此a≤5,
综合(i)(ii)a=5;
当a=5时A=B,则?x1<0,q′(x1)∈B=A,即?x2>0,使得q′(x2)=q′(x1)成立,
因为q′(x)在(0,+∞)上单调递增,所以x2的值是唯一的;
同理,?x1>0,即存在唯一的非零实数x2(x2≠x1),q′(x)在(0,+∞)上单调递增,
要使q′(x2)=q′(x1)成立,所以a=5满足题意.
点评:本题考查利用导数研究函数的极值、最值及恒成立问题,考查学生综合运用所学知识分析问题解决问题的能力,综合性强,难度大.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
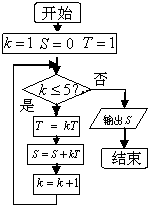 (2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )
(2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )