题目内容
(2013•蓟县二模)设f(x)=2x-2-x.若当θ∈[-
,0)时,f(m-
)+f(m2-3)>0恒成立,则实数m的取值范围是( )
| π |
| 2 |
| 1 |
| cosθ-1 |
分析:先判断f(x)的奇偶性、单调性,利用函数的性质把不等式中的符号“f”去掉,转化为具体不等式,进而把恒成立问题转化为函数最值解决即可.
解答:解:因为f(x)的定义域为R,且f(-x)=2-x-2x=-(2x-2-x)=-f(x),
所以f(x)为奇函数;
又易知f(x)=2x-2-x为增函数,
所以f(m-
)+f(m2-3)>0可化为f(m-
)>-f(m2-3)=f(3-m2),
也即m-
>3-m2,即m2+m-3>
在当θ∈[-
,0)时恒成立,
当θ∈[-
,0)时,cosθ∈[0,1),
≤-1,
所以m2+m-3>-1,解得m<-2或m>1,即实数m的取值范围为(-∞,-2)∪(1,+∞).
故选D.
所以f(x)为奇函数;
又易知f(x)=2x-2-x为增函数,
所以f(m-
| 1 |
| cosθ-1 |
| 1 |
| cosθ-1 |
也即m-
| 1 |
| cosθ-1 |
| 1 |
| cosθ-1 |
| π |
| 2 |
当θ∈[-
| π |
| 2 |
| 1 |
| cosθ-1 |
所以m2+m-3>-1,解得m<-2或m>1,即实数m的取值范围为(-∞,-2)∪(1,+∞).
故选D.
点评:本题考查函数的奇偶性、单调性及其应用,考查函数恒成立问题,考查学生分析问题解决问题的能力.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
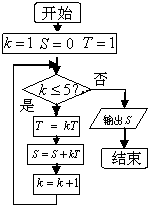 (2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )
(2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )