题目内容
(2013•蓟县二模)在正项等比数列{an}中,a2a4=4,S3=14,数列{bn}满足bn=log2an,则数列{bn}的前6项和是( )
分析:由等比数列的性质可知a2a4=a32=4,可求a3,然后结合S3=14,分别利用等比数列的通项及求和公式可利用首项a1和公比q表示,解方程可求a1,q,然后可求an,代入bn=log2an可求bn,进而可求和S6
解答:解:由等比数列的性质可知a2a4=a32=4,
又∵an>0
∴a3=2即a1q2=2①
∵S3=
=14,即a1(1+q+q2)=14②
②÷①可得
=7
解方程可得q=
或q=-
(舍)
∴a1=8,an=8•
=
∴bn=log2an=4-n
∴S6=3+2+1+0-1-2=3
故选C
又∵an>0
∴a3=2即a1q2=2①
∵S3=
| a1(1-q3) |
| 1-q |
②÷①可得
| q2+q+1 |
| q2 |
解方程可得q=
| 1 |
| 2 |
| 1 |
| 3 |
∴a1=8,an=8•
| 1 |
| 2n-1 |
| 1 |
| 2n-4 |
∴bn=log2an=4-n
∴S6=3+2+1+0-1-2=3
故选C
点评:本题主要考查了等比数列的性质及等比数列的求和公式、通项公式的简单应用.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
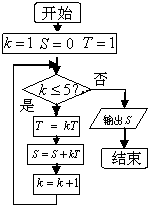 (2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )
(2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )