题目内容
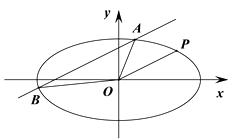
【题目】已知椭圆C的中心在坐标原点，焦点在x轴上，左顶点为A，左焦点为F1（﹣2，0），点B（2， 
）在椭圆C上，直线y=kx（k≠0）与椭圆C交于E，F两点，直线AE，AF分别与y轴交于点M，N
（Ⅰ）求椭圆C的方程；
（Ⅱ）在x轴上是否存在点P，使得无论非零实数k怎样变化，总有∠MPN为直角？若存在，求出点P的坐标，若不存在，请说明理由．
【答案】解：（Ⅰ）由题意可设椭圆方程为 
+ 
=1（a＞b＞0），
则c=2，a2﹣b2=c2， 
+ 
=1，解得：a2=8，b2=4．
可得椭圆C的方程为 
+ 
=1；
（Ⅱ）如图，设F（x0，y0），E（﹣x0，﹣y0），则 
+ 
=1，A（﹣2 
，0），
AF所在直线方程y= 
（x+2 ），
取x=0，得y= 
，
∴N（0， ），
AE所在直线方程为y= 
（x+2 ），
取x=0，得y= 
．
则以MN为直径的圆的圆心坐标为（0， 
），
半径r= 
，
圆的方程为x2+（y﹣ ）2= 
= 
，即x2+（y+ 
）2= ．
取y=0，得x=±2．
可得以MN为直径的圆经过定点（±2，0）．
可得在x轴上存在点P（±2，0），
使得无论非零实数k怎样变化，总有∠MPN为直角．
【解析】（1）根据焦点坐标得出c的值，再将B点的坐标代入椭圆方程，结合a2﹣b2=c2，即可解出a，b，c，从而得到椭圆方程，（2）设F（x0，y0），E（﹣x0，﹣y0），写出AE、AF所在直线方程，求出M、N的坐标，得到以MN为直径的圆的方程，由圆的方程可知以MN为直径的圆经过定点（±2，0），即可判断存在点P.
练习册系列答案
名校课堂系列答案
相关题目
