题目内容
6.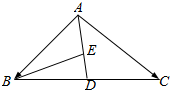 如图所示,在△ABC中,点D是边BC的中点,A,D,E三点共线,求证:存在一个实数λ,使得$\overrightarrow{AE}$=λ($\overrightarrow{AB}$+$\overrightarrow{AC}$)
如图所示,在△ABC中,点D是边BC的中点,A,D,E三点共线,求证:存在一个实数λ,使得$\overrightarrow{AE}$=λ($\overrightarrow{AB}$+$\overrightarrow{AC}$)
分析 利用向量的三角形法则,攻击已知,首先表示出$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,$\overrightarrow{AE}=μ\overrightarrow{AD}$,然后求出λ.
解答 证明:因为在△ABC中,点D是边BC色中点,A,D,E三点共线,
所以$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,$\overrightarrow{AE}=μ\overrightarrow{AD}$,
所以$\overrightarrow{AE}=\frac{μ}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,令$λ=\frac{μ}{2}$,
则存在一个实数λ,使得$\overrightarrow{AE}$=λ($\overrightarrow{AB}$+$\overrightarrow{AC}$).
点评 本题考查了平面向量的三角形法则的运用属于基础题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
11.若数列{an}满足:an+1=$\frac{1}{1{-a}_{n}}$,a8=2,则a1a2•…•a2015=( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -2 |
18.要得到y=sin2x-$\sqrt{3}$sin2x-cos2x的图象,只需将y=2sin2x的图象( )
| A. | 向左平移$\frac{5π}{12}$个单位 | B. | 向左平移$\frac{5π}{6}$个单位 | ||
| C. | 向右平移$\frac{5π}{12}$个单位 | D. | 向右平移$\frac{5π}{6}$个单位 |