题目内容
14.用“五点法“作出y=3sin($\frac{1}{2}$x-$\frac{π}{4}$)在一个周期上的简图.分析 用五点法求出对应的点的坐标,即可在坐标系中作出函数一个周期的图象.
解答  解:列表:
解:列表:
| x | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ | $\frac{9π}{2}$ |
| $\frac{1}{2}$x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| 3sin($\frac{1}{2}$x-$\frac{π}{4}$) | 0 | 3 | 0 | -3 | 0 |
点评 本题主要考查了三角函数的图象和性质,考查了五点作图法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列各组表示同一函数的是( )
| A. | y=x(x∈R)与y=x(x∈N) | B. | $y=\sqrt{x^2}$与$y={({\sqrt{x}})^2}$ | C. | y=1+$\frac{1}{x}$与u=1+$\frac{1}{v}$ | D. | y=x与$y=\frac{x^2}{x}$ |
19.已知p:$\left\{\begin{array}{l}{lg|x|≤1}\\{{2}^{x+2}≥1}\end{array}\right.$,q:x2-2x+1-m2≤0(m>0),若¬p是¬q的必要不充分条件,求实数m的取值范围( )
| A. | (-∞,9] | B. | [9,+∞) | C. | (-∞,3] | D. | [3,+∞) |
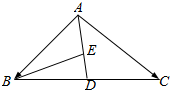 如图所示,在△ABC中,点D是边BC的中点,A,D,E三点共线,求证:存在一个实数λ,使得$\overrightarrow{AE}$=λ($\overrightarrow{AB}$+$\overrightarrow{AC}$)
如图所示,在△ABC中,点D是边BC的中点,A,D,E三点共线,求证:存在一个实数λ,使得$\overrightarrow{AE}$=λ($\overrightarrow{AB}$+$\overrightarrow{AC}$)