题目内容
18．要得到y=sin2x-$\sqrt{3}$sin2x-cos2x的图象，只需将y=2sin2x的图象（ ）| A． | 向左平移$\frac{5π}{12}$个单位 | B． | 向左平移$\frac{5π}{6}$个单位 | ||
| C． | 向右平移$\frac{5π}{12}$个单位 | D． | 向右平移$\frac{5π}{6}$个单位 |
分析 利用三角恒等变换化简所给的函数的解析式，再利用函数y=Asin（ωx+φ）的图象变换规律，得出结论．
解答 解：∵y=sin2x-$\sqrt{3}$sin2x-cos2x=-cos2x-$\sqrt{3}$sin2x=-2in（2x+$\frac{π}{6}$）=sin（2x-$\frac{5π}{6}$），
把y=2sin2x的图象向右平移$\frac{5π}{12}$个单位，可以得到y=sin2（x-$\frac{5π}{12}$）=sin（2x-$\frac{5π}{6}$）的图象，
故选：C．
点评 本题主要考查三角恒等变换，函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
相关题目
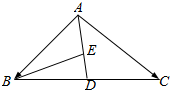如图所示，在△ABC中，点D是边BC的中点，A，D，E三点共线，求证：存在一个实数λ，使得$\overrightarrow{AE}$=λ（$\overrightarrow{AB}$+$\overrightarrow{AC}$）