题目内容
16.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosB-$\sqrt{3}$sinB)cosA=0.(1)求角A的大小.
(2)若b+c=1.求a的取值范围.
分析 (1)已知等式第一项利用诱导公式化简,第二项利用单项式乘多项式法则计算,整理后根据sinA不为0求出tanB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数;
(2)由b+c=1,利用基本不等式的性质化为bc≤$(\frac{b+c}{2})^{2}$=$\frac{1}{4}$,由余弦定理可得:a2=b2+c2-2bccosA=(b+c)2-2bc-bc=1-3bc,利用基本不等式的性质即可得出.
解答 解:(1)cosC+(cosB-$\sqrt{3}$sinB)cosA=0,
∴-cos(A+B)+cosAcosB-$\sqrt{3}$sinBcosA=0,
∴sinAsinB-$\sqrt{3}$sinBcosA=0,
∵sinB≠0,
∴sinA-$\sqrt{3}$cosA=0,
∵cosA≠0,
∴tanA=$\sqrt{3}$,
∵A∈(0,π).
解得A=$\frac{π}{3}$.
(2)∵b+c=1,
∴bc≤$(\frac{b+c}{2})^{2}$=$\frac{1}{4}$,
由余弦定理可得:a2=b2+c2-2bccosA=(b+c)2-2bc-bc=1-3bc≥1-$\frac{3}{4}$=$\frac{1}{4}$,当且仅当b=c=$\frac{1}{2}$时取等号.
又a<b+c=1.
∴a的取值范围是[$\frac{1}{2}$,1).
点评 本题考查了余弦定理、两角和差的正弦公式、诱导公式、三角函数的内角和定理、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.设向量$\overrightarrow{a}$=(-3,2),$\overrightarrow{b}$=(cosα,-$\frac{1}{3}$)(0°<α<180°),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则角α为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
6.若三点A(0,a,2b),B(2,3,4),C(3,4,5)共线,则下列等式成立的是( )
| A. | 2a=b | B. | a+b=2 | C. | 2a-b=3 | D. | a-2b=1 |
 如图所示,在△ABC中,点D是边BC的中点,A,D,E三点共线,求证:存在一个实数λ,使得$\overrightarrow{AE}$=λ($\overrightarrow{AB}$+$\overrightarrow{AC}$)
如图所示,在△ABC中,点D是边BC的中点,A,D,E三点共线,求证:存在一个实数λ,使得$\overrightarrow{AE}$=λ($\overrightarrow{AB}$+$\overrightarrow{AC}$)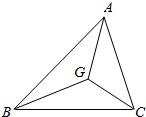 (1)如图,G是△ABC的重心,求证:$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$.
(1)如图,G是△ABC的重心,求证:$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$.