题目内容
已知对任意的平面向量,把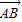 绕其起点沿逆时针方向旋转θ角,得到向量
绕其起点沿逆时针方向旋转θ角,得到向量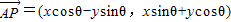 ,叫做把点B绕点A逆时针方向旋转θ角得到点P
,叫做把点B绕点A逆时针方向旋转θ角得到点P①已知平面内的点A(1,2),B
 ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转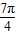 后得到点P,求点P的坐标
后得到点P,求点P的坐标②设平面内曲线C上的每一点绕逆时针方向旋转
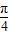 后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.
后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.
【答案】分析:①设P(x,y),则 ,
,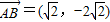 ,根据把点B绕点A沿逆时针方向旋转
,根据把点B绕点A沿逆时针方向旋转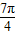 后得到点P,
后得到点P,
可得将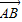 绕点A沿逆时针方向旋转
绕点A沿逆时针方向旋转 后得到
后得到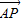 ,由此可得
,由此可得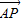 的坐标,从而可求点P的坐标
的坐标,从而可求点P的坐标
②利用旋转变换确定旋转前后,坐标之间的关系,利用已知曲线的方程,我们可以求出原来曲线C的方程.
解答:解:①设P(x,y),则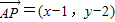 ,
,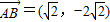 …(2分)
…(2分)
将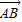 绕点A沿逆时针方向旋转
绕点A沿逆时针方向旋转 后得到
后得到 ,
,
所以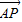 =
=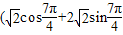 ,
,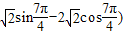 =(-1,-3)…(6分)
=(-1,-3)…(6分)
∴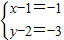 ,解得x=0,y=-1 …(7分)
,解得x=0,y=-1 …(7分)
∴点P的坐标为(0,-1)
②设平面内曲线C上的任一点Q(x,y),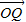 绕O逆时针方向旋转
绕O逆时针方向旋转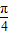 后得到的点Q′(x′,y′),则
后得到的点Q′(x′,y′),则
 …(10分)
…(10分)
即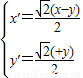 …(11分)
…(11分)
又x′2-y′2=1 …(12分)
∴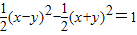 …(13分)
…(13分)
化简得: …(14分)
…(14分)
点评:本题考查新定义,考查旋转变换,利用旋转变换公式是我们解题的关键.
 ,
,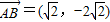 ,根据把点B绕点A沿逆时针方向旋转
,根据把点B绕点A沿逆时针方向旋转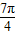 后得到点P,
后得到点P,可得将
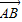 绕点A沿逆时针方向旋转
绕点A沿逆时针方向旋转 后得到
后得到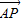 ,由此可得
,由此可得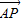 的坐标,从而可求点P的坐标
的坐标,从而可求点P的坐标②利用旋转变换确定旋转前后,坐标之间的关系,利用已知曲线的方程,我们可以求出原来曲线C的方程.
解答:解:①设P(x,y),则
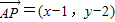 ,
,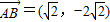 …(2分)
…(2分)将
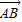 绕点A沿逆时针方向旋转
绕点A沿逆时针方向旋转 后得到
后得到 ,
,所以
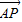 =
=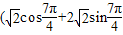 ,
,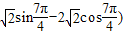 =(-1,-3)…(6分)
=(-1,-3)…(6分)∴
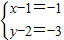 ,解得x=0,y=-1 …(7分)
,解得x=0,y=-1 …(7分)∴点P的坐标为(0,-1)
②设平面内曲线C上的任一点Q(x,y),
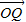 绕O逆时针方向旋转
绕O逆时针方向旋转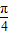 后得到的点Q′(x′,y′),则
后得到的点Q′(x′,y′),则 …(10分)
…(10分)即
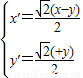 …(11分)
…(11分)又x′2-y′2=1 …(12分)
∴
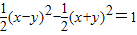 …(13分)
…(13分)化简得:
 …(14分)
…(14分)点评:本题考查新定义,考查旋转变换,利用旋转变换公式是我们解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
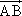 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转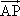 =(xcos
=(xcos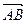 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转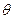 角,得到向量
角,得到向量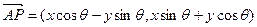 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转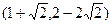 ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转 后得到点P,求点P的坐标
后得到点P,求点P的坐标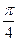 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线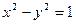 ,求原来曲线C的方程.
,求原来曲线C的方程. 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角,得到向量
角,得到向量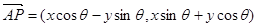 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转 ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转 后得到点P,求点P的坐标
后得到点P,求点P的坐标 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线 ,求原来曲线C的方程.
,求原来曲线C的方程.