题目内容
已知对任意的平面向量,把
绕其起点沿逆时针方向旋转θ角,得到向量
=(xcosθ-ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ角得到点P
①已知平面内的点A(1,2),B(1+
,2-2
),把点B绕点A沿逆时针方向旋转
后得到点P,求点P的坐标
②设平面内曲线C上的每一点绕逆时针方向旋转
后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.
| AB |
| AP |
①已知平面内的点A(1,2),B(1+
| 2 |
| 2 |
| 7π |
| 4 |
②设平面内曲线C上的每一点绕逆时针方向旋转
| π |
| 4 |
分析:①设P(x,y),则
=(x-1,y-2),
=(
,-2
),根据把点B绕点A沿逆时针方向旋转
后得到点P,
可得将
绕点A沿逆时针方向旋转
后得到
,由此可得
的坐标,从而可求点P的坐标
②利用旋转变换确定旋转前后,坐标之间的关系,利用已知曲线的方程,我们可以求出原来曲线C的方程.
| AP |
| AB |
| 2 |
| 2 |
| 7π |
| 4 |
可得将
| AB |
| 7π |
| 4 |
| AP |
| AP |
②利用旋转变换确定旋转前后,坐标之间的关系,利用已知曲线的方程,我们可以求出原来曲线C的方程.
解答:解:①设P(x,y),则
=(x-1,y-2),
=(
,-2
)…(2分)
将
绕点A沿逆时针方向旋转
后得到
,
所以
=(
cos
+2
sin
,
sin
-2
cos
)=(-1,-3)…(6分)
∴
,解得x=0,y=-1 …(7分)
∴点P的坐标为(0,-1)
②设平面内曲线C上的任一点Q(x,y),
绕O逆时针方向旋转
后得到的点Q′(x′,y′),则
…(10分)
即
…(11分)
又x′2-y′2=1 …(12分)
∴
(x-y)2-
(x+y)2=1…(13分)
化简得:y=-
…(14分)
| AP |
| AB |
| 2 |
| 2 |
将
| AB |
| 7π |
| 4 |
| AP |
所以
| AP |
| 2 |
| 7π |
| 4 |
| 2 |
| 7π |
| 4 |
| 2 |
| 7π |
| 4 |
| 2 |
| 7π |
| 4 |
∴
|
∴点P的坐标为(0,-1)
②设平面内曲线C上的任一点Q(x,y),
| OQ |
| π |
| 4 |
|
即
|
又x′2-y′2=1 …(12分)
∴
| 1 |
| 2 |
| 1 |
| 2 |
化简得:y=-
| 1 |
| 2x |
点评:本题考查新定义,考查旋转变换,利用旋转变换公式是我们解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
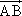 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转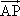 =(xcos
=(xcos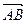 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转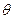 角,得到向量
角,得到向量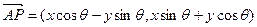 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转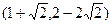 ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转 后得到点P,求点P的坐标
后得到点P,求点P的坐标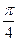 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线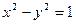 ,求原来曲线C的方程.
,求原来曲线C的方程. 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角,得到向量
角,得到向量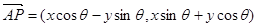 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转 ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转 后得到点P,求点P的坐标
后得到点P,求点P的坐标 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线 ,求原来曲线C的方程.
,求原来曲线C的方程.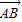 绕其起点沿逆时针方向旋转θ角,得到向量
绕其起点沿逆时针方向旋转θ角,得到向量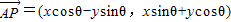 ,叫做把点B绕点A逆时针方向旋转θ角得到点P
,叫做把点B绕点A逆时针方向旋转θ角得到点P ,把点B绕点A沿逆时针方向旋转
,把点B绕点A沿逆时针方向旋转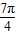 后得到点P,求点P的坐标
后得到点P,求点P的坐标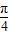 后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.
后得到的点的轨迹是曲线x2-y2=1,求原来曲线C的方程.