题目内容
如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.则矩形BNPM面积的最大值为 平方米.
【答案】分析:利用三角形的相似,可得函数的解析式及定义域,表示出面积,利用配方法,可得矩形BNPM面积的最大值.
解答:解:作PQ⊥AF于Q,所以PQ=8-y,EQ=x-4,
在△EDF中,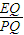 =
=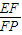 ,所以
,所以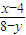 =
= .
.
所以y=- x+10,定义域为{x|4≤x≤8}.
x+10,定义域为{x|4≤x≤8}.
设矩形BNPM的面积为S,则S(x)=xy=x(10-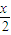 )=-
)=- (x-10)2+50.
(x-10)2+50.
所以S(x)是关于x的二次函数,且其开口向下,对称轴为x=10
所以当x∈[4,8],S(x)单调递增.
所以当x=8米时,矩形BNPM面积取得最大值48平方米.
故答案为:48.
点评:本题考查函数解析式的确定,考查配方法求函数的最值,考查学生的计算能力,属于中档题.
解答:解:作PQ⊥AF于Q,所以PQ=8-y,EQ=x-4,
在△EDF中,
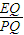 =
=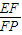 ,所以
,所以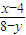 =
= .
.所以y=-
 x+10,定义域为{x|4≤x≤8}.
x+10,定义域为{x|4≤x≤8}.设矩形BNPM的面积为S,则S(x)=xy=x(10-
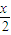 )=-
)=- (x-10)2+50.
(x-10)2+50.所以S(x)是关于x的二次函数,且其开口向下,对称轴为x=10
所以当x∈[4,8],S(x)单调递增.
所以当x=8米时,矩形BNPM面积取得最大值48平方米.
故答案为:48.
点评:本题考查函数解析式的确定,考查配方法求函数的最值,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
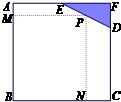 (2013•杨浦区一模)如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.则矩形BNPM面积的最大值为
(2013•杨浦区一模)如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.则矩形BNPM面积的最大值为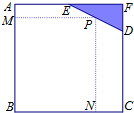 如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.求矩形BNPM面积的最大值.
如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.求矩形BNPM面积的最大值.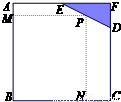
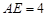 米,
米,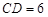 米. 为了合理利用这块钢板,将在五边形
米. 为了合理利用这块钢板,将在五边形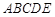 内截取一个矩形块
内截取一个矩形块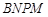 ,使点
,使点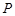 在边
在边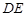 上. 则矩形
上. 则矩形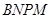 面积的最大值为____ 平方米 .
面积的最大值为____ 平方米 . 