题目内容
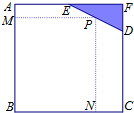 如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.求矩形BNPM面积的最大值.
如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.求矩形BNPM面积的最大值.分析:设AM=x,由题可知,BM=8-x,MP=4+2x且0≤x≤2,设矩形面积为S,则S=(4+2x)(8-x),再根据二次函数的性质,求得S的最大值.
解答:解:设AM=x,由题可知,BM=8-x,MP=4+2x且0≤x≤2,
设矩形面积为S,则S=(4+2x)(8-x),
即S=-2x2+12x+32=-2(x-3)2+50.
当x∈(-∞,3]时S递增,而[0,2]⊆(-∞,3],
∴当x=2时,S取最大值,Smax=48,此时点P在D处,
故当点P在D处时,矩形BNPM的面积最大,最大值为48平方米.
设矩形面积为S,则S=(4+2x)(8-x),
即S=-2x2+12x+32=-2(x-3)2+50.
当x∈(-∞,3]时S递增,而[0,2]⊆(-∞,3],
∴当x=2时,S取最大值,Smax=48,此时点P在D处,
故当点P在D处时,矩形BNPM的面积最大,最大值为48平方米.
点评:本题主要考查二次函数的性质,属于基础题.

练习册系列答案
相关题目
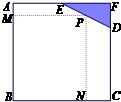 (2013•杨浦区一模)如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.则矩形BNPM面积的最大值为
(2013•杨浦区一模)如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.则矩形BNPM面积的最大值为
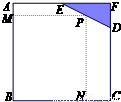
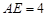 米,
米,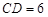 米. 为了合理利用这块钢板,将在五边形
米. 为了合理利用这块钢板,将在五边形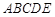 内截取一个矩形块
内截取一个矩形块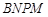 ,使点
,使点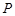 在边
在边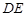 上. 则矩形
上. 则矩形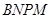 面积的最大值为____ 平方米 .
面积的最大值为____ 平方米 . 