题目内容
给出下列关于互不相同的直线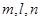 和平面
和平面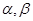 的四个命题:
的四个命题:
①若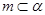 ,
,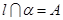 ,点
,点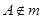 ,则
,则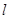 与
与 不共面;
不共面;
②若 、
、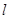 是异面直线,
是异面直线,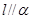 ,
,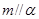 ,且
,且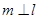 ,
, ,则
,则 ;
;
③若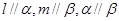 ,则
,则 ;
;
④若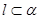 ,
,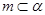 ,
,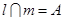 ,
, ,
, ,则
,则 .
.
其中为假命题的是( )
| A.① | B.② | C.④ | D.③ |
D
解析试题分析:对于命题①,假设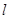 与
与 共面,则直线
共面,则直线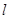 与
与 平行或相交,由于
平行或相交,由于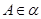 ,
,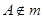 ,则点
,则点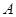 和直线
和直线 确定平面
确定平面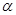 ,又直线
,又直线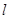 与
与 共面,则直线
共面,则直线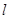 与
与 确定平面
确定平面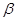 ,则直线
,则直线 为平面
为平面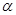 与平面
与平面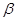 的交线,由于
的交线,由于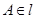 而
而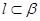 ,所以
,所以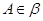 ,由公理
,由公理 可知,
可知,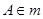 ,这与
,这与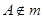 矛盾,故假设不成立,故
矛盾,故假设不成立,故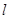 与
与 不共面,命题①为真命题;对于命题②,因为
不共面,命题①为真命题;对于命题②,因为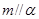 ,则在平面
,则在平面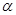 存在直线
存在直线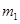 ,使得
,使得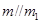 ,同理,在平面内存在直线
,同理,在平面内存在直线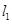 ,使得
,使得 ,由于直线
,由于直线 与直线
与直线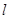 为异面直线,则
为异面直线,则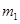 与
与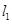 相交,
相交,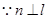 且
且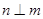 ,所以
,所以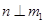 且
且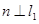 ,由于
,由于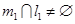 ,所以
,所以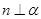 ;对于命题③,如
;对于命题③,如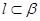 ,
,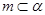 ,当
,当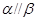 时,
时,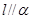 ,
,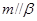 ,但是直线
,但是直线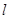 与
与 无交点,则直线
无交点,则直线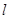 与
与 平行或异面,故命题③错误;对于命题④,由平面与平面平行的判定定理可知命题④正确,故选D.
平行或异面,故命题③错误;对于命题④,由平面与平面平行的判定定理可知命题④正确,故选D.
考点:空间中点、线、面的位置关系

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
四棱锥P-ABCD中,底面ABCD是平行四边形,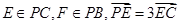 ,
,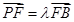 ,若
,若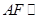 平面BDE,则
平面BDE,则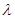 的值为 ( )
的值为 ( )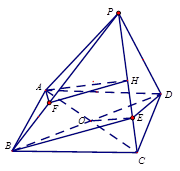
| A.1 | B.3 | C.2 | D.4 |
已知m和n是两条不同的直线,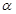 和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( )
和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( )
A.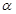 ⊥β且 ⊥β且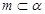 | B.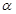 ⊥β且 ⊥β且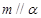 |
C.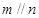 且n⊥β 且n⊥β | D.m⊥n且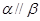 |
已知α,β,γ是三个不同的平面,α∩γ=m,β∩γ=n.则( )
| A.若m⊥n,则α⊥β | B.若α⊥β,则m⊥n |
| C.若m∥n,则α∥β | D.若α∥β,则m∥n |
如图,在空间直角坐标系中,正方体 的棱长为1,
的棱长为1, ,则
,则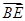 等于( )
等于( )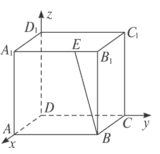
A. | B. 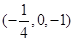 | C. | D.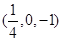 |
已知点B是点A(3,4,-2)在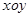 平面上的射影,则等于( )
平面上的射影,则等于( )
A. | B.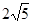 | C.5 | D. |
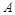
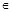 平面
平面 若
若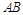 与
与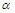 所成角正弦值为0.8,
所成角正弦值为0.8, 与
与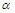 成450角,则
成450角,则 距离的范围( )
距离的范围( )
A.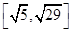 | B. |
C.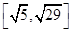 | D.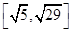 ∪ ∪ |



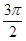

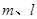 ,平面
,平面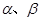 ,且
,且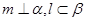 ,给出下列命题:
,给出下列命题: 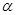 ∥
∥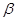 ,则m⊥
,则m⊥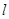 ; ②若
; ②若