题目内容
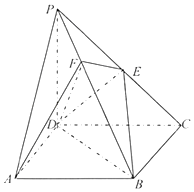
【题目】在三棱柱ABC﹣A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1 , A1A1的中点,点F在棱AB上,且AF= ![]() AB.
AB.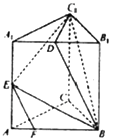
(1)求证:EF∥平面BDC1;
(2)求三棱锥D﹣BEC1的体积.
【答案】
(1)解:取AB的中点O,连接A1O,
∵AF= ![]() AB,
AB,
∴F为AO的中点,又E为AA1的中点,
∴EF∥A1O,
∵A1D= ![]() ,BO=
,BO= ![]() ,AB
,AB ![]() A1B1,
A1B1,
∴A1D ![]()
∴四边形A1DBO为平行四边形,
∴A1O∥BD,
∴EF∥BD,又EF平面BDC1,BD平面BDC1,
∴EF∥平面BDC1.
(2)∵AA1⊥平面A1B1C1,C1D平面A1B1C1,
∴AA1⊥C1D,
∵A1C1=B1C1=A1B1=2,D为A1B1的中点,
∴C1D⊥A1B1,C1D= ![]() ,
,
又AA1平面AA1B ![]() B,A1B1平面AA1B
B,A1B1平面AA1B ![]() B,AA1∩A1B1=A1,
B,AA1∩A1B1=A1,
∴C1D⊥平面AA1B1B,
∵AB=AA1=2,D,E分别为A1B1,AA1的中点,
∴S△BDE=22﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() .
.
∴V ![]() =V
=V ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)根据线面平行的判定定理证明即可;(2)证明![]() ,求出棱锥的底面面积,然后求解即可.
,求出棱锥的底面面积,然后求解即可.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.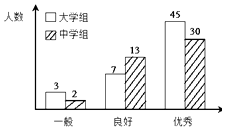
(Ⅰ)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:K2 ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(k2≥k0) | 0.10 | 0.05 | 0.005 |
k0 | 2.706 | 3.841 | 7.879 |
(Ⅱ)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
(Ⅲ)如果在优秀等级的选手中取4名,在良好等级的选手中取2名,再从这6人中任选3人组成一个比赛团队,求所选团队中的有2名选手的等级为优秀的概率.