题目内容
19.已知某几何体的一条棱长为m,在正视图中的投影长为$\sqrt{6}$,在侧视图与俯视图中的投影长为a与b,且a+b=4,则m的最小值为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
分析 根据三视图的定义,构造一个长方体,利用长方体的边长关系进行求解即可.
解答 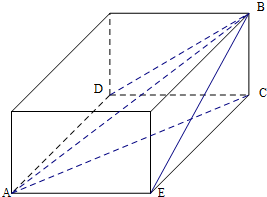 解:设几何体的棱为AB,则AB=m,
解:设几何体的棱为AB,则AB=m,
在长方体中,BD为正投影,
BE为侧视图中的投影,
AC为俯视图中的投影,
则BD=$\sqrt{6}$,BE=a,AC=b且满足a+b=4,
设AE=x,CE=y,BC=z,
则满足x2+y2+z2=m2,
x2+y2=b2,①y2+z2=a2,②x2+2z=6,③,
三式相加得2(x2+y2+z2)=a2+b2+6,
即2m2=a2+b2+6=(a+b)2+6-2ab=16+6-2ab=22-2ab,
∵4=a+b$≥2\sqrt{ab}$,
∴ab≤4,-ab≥-4,
则2m2=22-2ab≥22-8=14,
即m2≥7,
则m≥$\sqrt{7}$,当且仅当a=b=2时,取等号,
故m的最小值为$\sqrt{7}$,
故选:D.
点评 本题主要考查空间三视图的应用以及利用基本不等式进行求解最值问题,根据条件构造一个长方体是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
9.sin$\frac{5π}{6}$的值等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
4.$\underset{lim}{x→0}$$\frac{{∫}_{0}^{x}ln(cost)dt}{{x}^{3}}$=( )
| A. | 0 | B. | $\frac{1}{6}$ | C. | -$\frac{1}{6}$ | D. | ∞ |
5.已知θ是第二象限的角,且sin$\frac{θ}{2}$<cos$\frac{θ}{2}$,那么sin$\frac{θ}{2}$+cos$\frac{θ}{2}$的取值范围是( )
| A. | (-1,0) | B. | (1,$\sqrt{2}$) | C. | (-1,1) | D. | (-$\sqrt{2}$,-1) |

