题目内容
【题目】自驾游从
地到
地有甲乙两条线路，甲线路是
，乙线是
，其中
段、
段、
段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表1所示.经调查发现，堵车概率
在
上变化， 
在
上变化.在不堵车的情况下.走线路甲需汽油费500元，走线路乙需汽油费545元.而每堵车1小时，需多花汽油费20元.路政局为了估计
段平均堵车时间，调查了100名走甲线路的司机，得到表2数据.
CD段 | EF段 | GH段 | |||
堵车概率 |
|
|
| ||
平均堵车时间 （单位：小时） |
| 2 | 1 | ||
（表1） | |||||
堵车时间（单位：小时） | 频数 | ||||
| 8 | ||||
| 6 | ||||
| 38 | ||||
| 24 | ||||
| 24 | ||||
（表2） | |||||
（1）求
段平均堵车时间
的值.
（2）若只考虑所花汽油费期望值的大小，为了节约，求选择走甲线路的概率.
（3）在(2)的条件下，某4名司机中走甲线路的人数记为X，求X的数学期望。
【答案】（1）
（2）
（3）
【解析】试题分析：（1）用每一段的时间的平均值乘以对应的概率，即为所求；（2）先求出走线路甲所花汽油费的期望
，再求出走乙线路多花汽油费的数学期望为
．择走甲线路应满足
，结合
、
的范围，利用几何概型求出选择走甲线路的概率；（3）根据二项分布的特征求其期望.
试题解析：（1） 
（2）设走线路甲所花汽油费为
元，则
法一：设走乙线路多花的汽油费为
元， 
段、
段堵车与否相互独立，
， 
， 
， 
走乙线路所花汽油费的数学期望为
依题意选择走甲线路应满足
，
（3）二项分布
每日10分钟口算心算速算天天练系列答案
【题目】假设关于某设备使用年限x（年）和所支出的维修费用y（万元）有如下统计资料：
2 | 3 | 4 | 5 | 6 | |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知，y对x呈线性相关关系，试求：
（Ⅰ）请画出上表数据的散点图；
（Ⅱ）请根据上表提供的数据，求出y关于x的线性回归方程
=bx+
；
（Ⅲ）估计使用年限为10年时，维修费用约是多少？
（参考数据：2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3）
【题目】随着移动互联网的快速发展，基于互联网的共享单车应运而生．某市场研究人员为了了解共享单车运营公司M的经营状况，对该公司最近六个月内的市场占有率进行了统计，并绘制了相应的折线图．
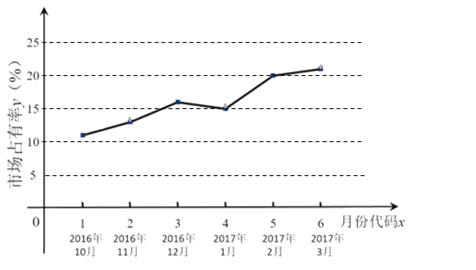
（Ⅰ）由折线图可以看出，可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系．求y关于x的线性回归方程，并预测M公司2017年4月份（即x=7时）的市场占有率；
（Ⅱ）为进一步扩大市场，公司拟再采购一批单车．现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择，按规定每辆单车最多使用4年，但由于多种原因（如骑行频率等）会导致车辆报废年限各不相同．考虑到公司运营的经济效益，该公司决定先对两款车型的单车各100辆进行科学模拟测试，得到两款单车使用寿命频数表如下：
车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 20 | 35 | 35 | 10 | 100 |
B | 10 | 30 | 40 | 20 | 100 |
经测算，平均每辆单车每年可以带来收入500元．不考虑除采购成本之外的其他成本，假设每辆单车的使用寿命都是整数年，且以频率作为每辆单车使用寿命的概率．如果你是M公司的负责人，以每辆单车产生利润的期望值为决策依据，你会选择采购哪款车型？
参考数据： 
（参考公式：回归直线方程为
，其中
）