题目内容
【题目】如图,将正六边形ABCDEF中的一半图形ABCD绕AD翻折到AB1C1D,使得∠B1AF=60°.G是BF与AD的交点.
(Ⅰ)求证:平面ADEF⊥平面B1FG;
(Ⅱ)求直线AB1与平面ADEF所成角的正弦值.
【答案】证明:(Ⅰ)由正六边形对称性可知BF⊥AD, 因此B1G⊥AD,FG⊥AD.
又B1G∩FG=G,B1G平面B1GF,FG平面B1GF,
所以AD⊥平面B1GF.
又因为AD平面ADEF,
所以平面ADEF⊥平面B1FG.
(Ⅱ)(方法一)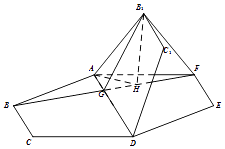
由(Ⅰ)已得平面B1GF⊥平面ADEF.
作B1H⊥FG于H,
又由于平面B1GF∩平面ADEF=FG,
所以B1H⊥平面ADEF.
连接AH,则∠B1AH就是直线B1A与平面ADEF所成的角.
不妨设正六边形边长为2.
则AF=AB1=2且∠B1AF=60°,∠B1AG=∠FAG=60°
得B1F=2, ![]() .
.
在△B1GF中, ![]() =
= 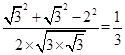 .
.![]() .
. ![]() ,
,![]() ,
,
所以直线AB1与平面ADEF所成角的正弦值为 ![]() .
.
(方法二)如图,以A为坐标原点,以AD为x轴,
过A在平面ADEF内作垂直于AD的直线为y轴,
过A作垂直于平面ADEF的直线为z轴建立空间直角坐标系.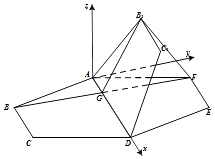
不妨设正六边形边长为2.则 ![]() ,
, ![]() ,
,
设 ![]() .
.
由 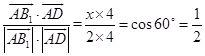
得x①.
由 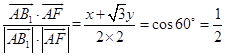 得
得 ![]() ②.
②.
又 ![]() ③.
③.
由①②③得 ![]() .所以
.所以 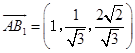 .
.
取平面ADEF的法向量 ![]() .
. 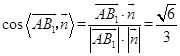 .
.
所以直线AB1与平面ADEF所成角的正弦值为 ![]()
【解析】(Ⅰ)推导出B1G⊥AD,FG⊥AD,从而AD⊥平面B1GF,由此能证明平面ADEF⊥平面B1FG.(Ⅱ)法一:作B1H⊥FG于H,连接AH,则∠B1AH就是直线B1A与平面ADEF所成的角,由此能求出直线AB1与平面ADEF所成角的正弦值.法二:以A为坐原点,以AD为x轴,过A在平面ADEF内作垂直于AD的直线为y轴,过A作垂直于平面ADEF的直线为z轴建立空间直角坐标系,利用向量法能求出直线AB1与平面ADEF所成角的正弦值为 ![]() .
.
【考点精析】根据题目的已知条件,利用异面直线及其所成的角和平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一个平面过另一个平面的垂线,则这两个平面垂直.

【题目】某校举行环保知识竞赛,为了了解本次竞赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为正数,满分100分),进行统计,请根据频率分布表中所提供的数据,解答下列问题:
(Ⅰ)求a、b的值;
(Ⅱ)若从成绩较好的第3、4、5组中,按分层抽样的方法抽取6人参加社区志愿者活动,并从中选出2人做负责人,求2人中至少有1人是第四组的概率.
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60] | 5 | 0.05 |
第2组 | [60,70] | a | 0.35 |
第3组 | [70,80] | 30 | b |
第4组 | [80,90] | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 | |