题目内容
甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人5次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用茎叶图表示这两组数据;.
(2)现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(3)若从甲、乙两人的5次成绩中各随机抽取一个,求甲的成绩比乙高的概率.
(1)茎叶图见解析;(2)乙;(3)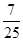 .
.
解析试题分析:(1)茎叶图是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少。 在制作茎叶图时,重复出现的数据要重复记录,不能遗漏,特别是“叶”部分,同一数据出现几次,就要在图中体现几次;(2)可计算出两人的平均成绩,方差(以说明他的稳定性),最高成绩等数据,然后比较得出结论;(3)甲乙两人各5个数据,因此各抽取一个,可以用列举法列出所有情形,共25个,然后在其中观察计数甲比乙大的组合,有7个,那么所求概率为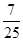 .
.
试题解析:(1)茎叶图  3分
3分
(2)由图可知,乙的平均成绩大于甲的平均成绩,且乙的方差小于甲的方差,且乙的最高分高于甲的最高分,因此应选派乙参赛更好. 6分
(3)记事件A: 甲的成绩比乙高从甲、乙两人5次的成绩中各随机抽取一个成绩,所有的基本事件如下: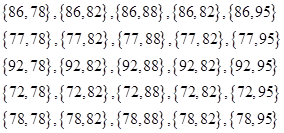
共25个. 9分
事件 包含的基本事件有
包含的基本事件有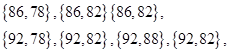 共7个 11分
共7个 11分
 13分
13分
考点:(1)茎叶图;(2)样本数据的特征;(3)古典概型.

 名校课堂系列答案
名校课堂系列答案从一批苹果中,随机抽取50个,其重量(单位:g)的频数分布表如下:
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有一个的概率.
通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
| | 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
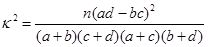
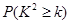 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
试考查大学生“爱好该项运动是否与性别有关”,若有关,请说明有多少把握。
某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(2)在该样品的一等品中,随机抽取两件产品,
(1)用产品编号列出所有可能的结果;
(2)设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率
为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日期 | 1月 10日 | 2月 10日 | 3月 10日 | 4月 10日 | 5月 10日 | 6月 10日 |
| 昼夜温差 x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数 y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
(1)求选取的2组数据恰好是相邻两个月的概率.
(2)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程
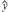 =
= x+
x+ .
.(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式:
 =
=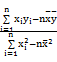 =
=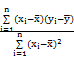 ,
, =
= -
-
 ).
).  小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段 ,
, ,
, ,
, ,
, (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示. 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量 .
.
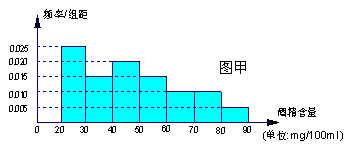
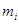 与
与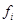 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率) 
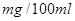 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90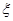 为吴、李两位先生被抽中的人数,求
为吴、李两位先生被抽中的人数,求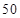 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为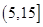 ,
,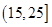 ,
,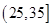 ,
, ,由此得到样本的重量频率分布直方图,如图
,由此得到样本的重量频率分布直方图,如图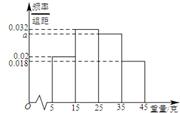
 的值;
的值; 组的频率为
组的频率为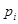 ,第
,第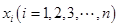 ,则样本数据的平均值为
,则样本数据的平均值为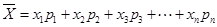 .)
.) 个小球,其中重量在
个小球,其中重量在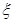 ,求
,求