题目内容
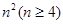 个正数排成
个正数排成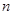 行
行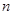 列:
列: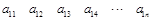
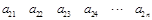
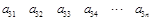
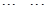
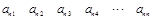
其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知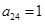 ,
,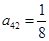 ,
,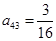 ,则
,则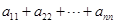 = 。
= 。
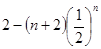
解析试题分析:设a11=a,第一行数的公差为d,第一列数的公比为q,可得ast=[a+(t-1)d]qs-1,又设第一行数列公差为d,各列数列的公比为q,则第四行数列公差是dq3,于是可得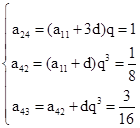 ,
,
解此方程组,得a11=d=q=±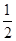 ,由于给n2个数都是正数,必有q>0,从而有a11=d=q=
,由于给n2个数都是正数,必有q>0,从而有a11=d=q=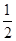 ,
,
于是对任意的1≤k≤n,有akk=a1kqk-1=[a11+(k-1)d]qk-1=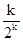 ,
,
得S=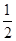 +
+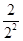 +……+
+……+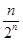 ,
,
又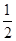 S=
S=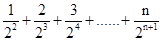 。
。
两式相减后得: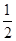 S=
S=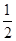 +
+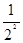 +……+
+……+ ,
,
所以S=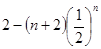 。
。
考点:本题主要考查等差数列、等比数列的基础知识,“错位相减法”。
点评:难题,通过观察数列的特征,布列方程组,先求出数列的通项,从而根据数列通项的特点选择合适的求和方法。“分组求和法”“裂项相消法”也常常考到的求和方法。

练习册系列答案
相关题目
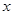 ,用
,用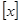 表示不超过
表示不超过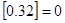 ,
,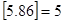 ,若
,若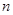 为正整数,
为正整数,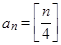 ,
,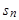 为数列
为数列 的前
的前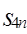 __________________________;
__________________________; 对任意正整数n都成立,且
对任意正整数n都成立,且 ,则
,则 。
。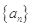 中,
中, 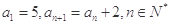 ,那么此数列的前10项和
,那么此数列的前10项和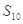 = .
= .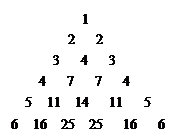
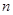 行首尾两数均为
行首尾两数均为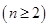 第
第 个数是
个数是  第2个数是_________.
第2个数是_________. 的首项为
的首项为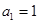 ,且
,且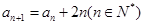 ,则这个数列的通项公式为___________
,则这个数列的通项公式为___________ 的前
的前 项和
项和 ,数列
,数列 满足
满足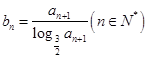 .
.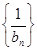 的前
的前 .
. 中,
中, ,且对于任意正整数n,都有
,且对于任意正整数n,都有 ,则
,则 =______
=______