题目内容
已知二阶矩阵M有特征值 及对应的一个特征向量
及对应的一个特征向量 ,且M
,且M =
= .求矩阵M.
.求矩阵M.
 及对应的一个特征向量
及对应的一个特征向量 ,且M
,且M =
= .求矩阵M.
.求矩阵M.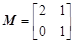
试题分析:根据题意结合矩阵运算可得:
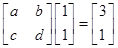 ,再由特征向量的定义可得:
,再由特征向量的定义可得: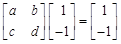 ,这样可得关于a,b,c,d的一个四元一次方程组,即可求解.
,这样可得关于a,b,c,d的一个四元一次方程组,即可求解.试题解析:设
 ,则由
,则由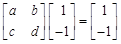 ,得
,得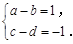
再由
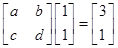 ,得
,得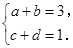
联立以上方程组解得a=2,b=1,c=0,d=1,故
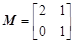 . 10分
. 10分
练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
题目内容
 及对应的一个特征向量
及对应的一个特征向量 ,且M
,且M =
= .求矩阵M.
.求矩阵M.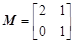
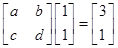 ,再由特征向量的定义可得:
,再由特征向量的定义可得: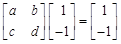 ,这样可得关于a,b,c,d的一个四元一次方程组,即可求解.
,这样可得关于a,b,c,d的一个四元一次方程组,即可求解. ,则由
,则由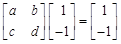 ,得
,得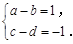
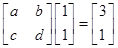 ,得
,得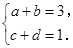
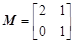 . 10分
. 10分
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案