题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:由 |
(2) |
解:由 当 当 |
(3) |
解:当
|

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
| |||||||||||
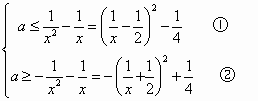 对于任意的
对于任意的