题目内容
定义平面向量的一种运算:a b=|a||b|sin 〈a,b〉,则下列命题:①a
b=|a||b|sin 〈a,b〉,则下列命题:①a b=b
b=b a;②λ(a
a;②λ(a b)=(λa)
b)=(λa)  b;③(a+b)?c=(a
b;③(a+b)?c=(a c)+(b
c)+(b c);④若a=(x1,y1),b=(x2,y2),则a
c);④若a=(x1,y1),b=(x2,y2),则a b=|x1y2-x2y1|.其中真命题是________________________(写出所有真命题的序号).
b=|x1y2-x2y1|.其中真命题是________________________(写出所有真命题的序号).
 b=|a||b|sin 〈a,b〉,则下列命题:①a
b=|a||b|sin 〈a,b〉,则下列命题:①a b=b
b=b a;②λ(a
a;②λ(a b)=(λa)
b)=(λa)  b;③(a+b)?c=(a
b;③(a+b)?c=(a c)+(b
c)+(b c);④若a=(x1,y1),b=(x2,y2),则a
c);④若a=(x1,y1),b=(x2,y2),则a b=|x1y2-x2y1|.其中真命题是________________________(写出所有真命题的序号).
b=|x1y2-x2y1|.其中真命题是________________________(写出所有真命题的序号).①④
由定义知b a=|b||a|sin 〈a,b〉=a
a=|b||a|sin 〈a,b〉=a b,所以①正确.②当λ<0时,〈λa,b〉=π-〈a,b〉,所以
b,所以①正确.②当λ<0时,〈λa,b〉=π-〈a,b〉,所以 ?b=|λa||b|sin 〈λa,b〉=-λ|a||b|sin 〈a·b〉,而λ(a
?b=|λa||b|sin 〈λa,b〉=-λ|a||b|sin 〈a·b〉,而λ(a b)=λ|a||b|sin 〈a,b〉,所以②不成立.③因为a+b=0显然不成立,所以③不成立.④(a
b)=λ|a||b|sin 〈a,b〉,所以②不成立.③因为a+b=0显然不成立,所以③不成立.④(a b)2=|a|2·|b|2sin 2〈a,b〉=|a|2·|b|2(1-cos 2〈a,b〉)=|a|2·|b|2-|a|2·|b|2cos 2〈a,b〉=|a|2·|b|2-(a·b)2=
b)2=|a|2·|b|2sin 2〈a,b〉=|a|2·|b|2(1-cos 2〈a,b〉)=|a|2·|b|2-|a|2·|b|2cos 2〈a,b〉=|a|2·|b|2-(a·b)2= -
-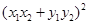 =
= ,所以a
,所以a b=|x1y2-x2y1|,所以④成立.
b=|x1y2-x2y1|,所以④成立.
 a=|b||a|sin 〈a,b〉=a
a=|b||a|sin 〈a,b〉=a b,所以①正确.②当λ<0时,〈λa,b〉=π-〈a,b〉,所以
b,所以①正确.②当λ<0时,〈λa,b〉=π-〈a,b〉,所以 ?b=|λa||b|sin 〈λa,b〉=-λ|a||b|sin 〈a·b〉,而λ(a
?b=|λa||b|sin 〈λa,b〉=-λ|a||b|sin 〈a·b〉,而λ(a b)=λ|a||b|sin 〈a,b〉,所以②不成立.③因为a+b=0显然不成立,所以③不成立.④(a
b)=λ|a||b|sin 〈a,b〉,所以②不成立.③因为a+b=0显然不成立,所以③不成立.④(a b)2=|a|2·|b|2sin 2〈a,b〉=|a|2·|b|2(1-cos 2〈a,b〉)=|a|2·|b|2-|a|2·|b|2cos 2〈a,b〉=|a|2·|b|2-(a·b)2=
b)2=|a|2·|b|2sin 2〈a,b〉=|a|2·|b|2(1-cos 2〈a,b〉)=|a|2·|b|2-|a|2·|b|2cos 2〈a,b〉=|a|2·|b|2-(a·b)2= -
-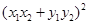 =
= ,所以a
,所以a b=|x1y2-x2y1|,所以④成立.
b=|x1y2-x2y1|,所以④成立.
练习册系列答案
相关题目
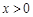 ,则
,则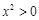 ”的否命题为 .
”的否命题为 .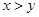 ,则
,则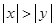 ”的否命题是:__________________.
”的否命题是:__________________.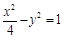 的渐近线方程是
的渐近线方程是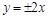 . 则 ( )
. 则 ( )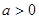 ,
,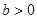 ,则有
,则有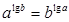 成立;
成立;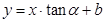 的倾斜角等于
的倾斜角等于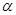 ;
;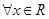 ,
, ”的否定是 .
”的否定是 .