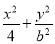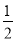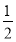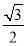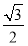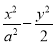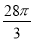题目内容
设椭圆M: =1(a>
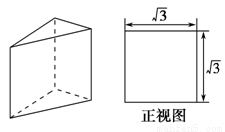
=1(a>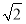 )的右焦点为F1,直线l:x=
)的右焦点为F1,直线l:x=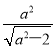 与x轴交于点A,若
与x轴交于点A,若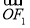 1=2
1=2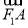 (其中O为坐标原点).
(其中O为坐标原点).
(1)求椭圆M的方程;
(2)设P是椭圆M上的任意一点,EF为圆N:x2+(y-2)2=1的任意一条直径(E,F为直径的两个端点),求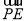 ·
·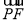 的最大值.
的最大值.
(1)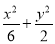 =1.(2)11.
=1.(2)11.
【解析】(1)由题设知,A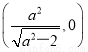 ,F1
,F1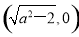 ,由
,由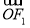 =2
=2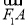 ,
,
得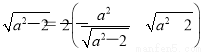 ,解得a2=6.
,解得a2=6.
所以椭圆M的方程为M: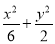 =1.
=1.
(2)设圆N:x2+(y-1)2=1的圆心为N,
则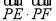 =(
=(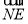 -
-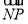 )·(
)·(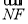 -
-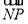 )=(-
)=(-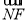 -
-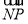 )·(
)·(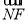 -
-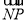 )=
)=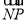 2-
2-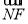 2=
2=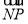 2-1.
2-1.
从而求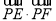 的最大值转化为求
的最大值转化为求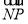 2的最大值.
2的最大值.
因为P是椭圆M上的任意一点,设P(x0,y0),所以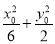 =1,
=1,
即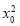 =6-3
=6-3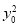 ,因为点N (0,2),所以
,因为点N (0,2),所以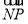 2=
2=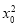 +(y0-2)2=-2(y0+1)2+12.
+(y0-2)2=-2(y0+1)2+12.
因为y0∈[-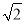 ,
,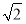 ],所以当y0=-1时,
],所以当y0=-1时,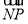 2取得最大值12.所以
2取得最大值12.所以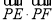 的最大值为11.
的最大值为11.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目