题目内容
【题目】2019年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,按阅读时间分组:第一组[0,5), 第二组[5,10),第三组[10,15),第四组[15,20),第五组[20,25],绘制了频率分布直方图如下图所示。已知第三组的频数是第五组频数的3倍。
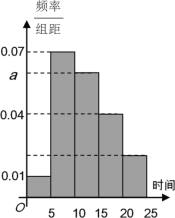
(1)求![]() 的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;
的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;
(2)现从第三、四、五这3组中用分层抽样的方法抽取6人参加校“中华诗词比赛”。经过比赛后,从这6人中随机挑选2人组成该校代表队,求这2人来自不同组别的概率。
【答案】(1)a=0.06,平均值为12.25小时 (2)![]()
【解析】
(1)由频率分布直方图可得第三组和第五组的频率之和,第三组的频率,由此能求出a和该样本数据的平均数,从而可估计该校学生一周课外阅读时间的平均值;
(2)从第3、4、5组抽取的人数分别为3、2、1,设为A,B,C,D,E,F,利用列举法能求出从该6人中选拔2人,从而得到这2人来自不同组别的概率.
(1)由频率分布直方图可得第三组和第五组的频率之和为
![]() ,
,
第三组的频率为![]()
∴![]()
该样本数据的平均数
![]()
所以可估计该校学生一周课外阅读时间的平均值为![]() 小时。
小时。
(2)易得从第3、4、5组抽取的人数分别为3、2、1,
设为![]() ,则从该6人中选拔2人的基本事件有:
,则从该6人中选拔2人的基本事件有:
![]()
![]()
![]()
共15种,
其中来自不同的组别的基本事件有:
![]()
![]()
![]() ,
,
共11种,
∴这2人来自不同组别的概率为![]() .
.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目



