Question

【题目】如图，在四棱锥P－ABCD中，PA⊥底面ABCD，底面ABCD为梯形，AD∥BC，CD⊥BC，AD＝2，AB＝BC＝3，PA＝4，M为AD的中点，N为PC上一点，且PC＝3PN.

(1)求证：MN∥平面PAB；

(2)求二面角PANM的余弦值．

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：（1）作NH∥BC，根据平几知识可得AMNH为平行四边形，即得MN∥AH. 再根据线面平行判定定理得结论（2）先根据空间直角坐标系，再设立各点坐标，根据方程组解得平面法向量，根据向量数量积求向量夹角，最后根据二面角与向量夹角相等或互补关系得结果．

试题解析：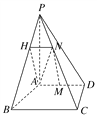

(1)证明：在平面PBC内作NH∥BC交PB于点H，连接AH，

在△PBC中，NH∥BC，且NH＝BC＝1，AM＝AD＝1.

∵AD∥BC，∴NH∥AM，且NH＝AM，

∴四边形AMNH为平行四边形，∴MN∥AH.

∵AH平面PAB，MN平面PAB，∴MN∥平面PAB.

(2)解：在平面ABCD内作AE∥CD交BC于E，则AE⊥AD.

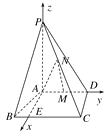
分别以AE，AD，AP所在直线为x轴、y轴、z轴建立空间直角坐标系A－xyz，则P(0,0,4)，M(0,1,0)，C(2，2,0)，N.

设平面AMN的法向量m＝(x，y，z)，＝(0,1,0)，＝，

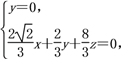则取m＝.

设平面PAN的法向量n＝(x，y，z)，＝(0,0,4)，＝，

则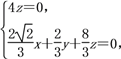取n＝(1，－，0)，

则cos〈m，n〉＝＝，故二面角PANM的余弦值为.