题目内容
已知函数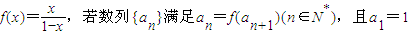 .
.(I)求证:数列
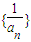 是等差数列;
是等差数列;(II)令bn=anan+1(n∈N*),设数列{bn}的前n项和为Sn,求使得
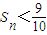 成立的n的最大值.
成立的n的最大值.
【答案】分析:(I)将条件an=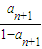 变形得
变形得 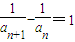 ,根据等差数列的定义可知数列
,根据等差数列的定义可知数列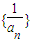 是等差数列;
是等差数列;
(II)由(I)知求出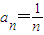 ,从而求出bn,然后利用裂项求和法求出{bn}的前n项和,根据
,从而求出bn,然后利用裂项求和法求出{bn}的前n项和,根据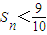 建立不等式,解之即可求出n的最值范围,即可求出所求.
建立不等式,解之即可求出n的最值范围,即可求出所求.
解答:解:(I)由an=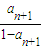 ⇒
⇒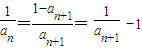 得
得 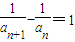
∴数列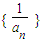 是首项为
是首项为 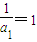 ,公差为1的等差数列
,公差为1的等差数列
(II)由(I)知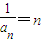 ,
,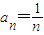 ∴
∴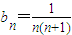 =
=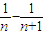
∴{bn}的前n项和为: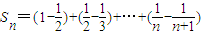 =1-
=1-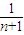
由题知1-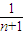 <
<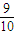 解得n<9所以n的最大值为8.
解得n<9所以n的最大值为8.
点评:本题主要考查了等差数列的判定,以及利用裂项求和法进行求和,同时考查了不等式的解法,属于中档题.
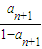 变形得
变形得 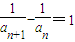 ,根据等差数列的定义可知数列
,根据等差数列的定义可知数列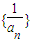 是等差数列;
是等差数列;(II)由(I)知求出
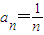 ,从而求出bn,然后利用裂项求和法求出{bn}的前n项和,根据
,从而求出bn,然后利用裂项求和法求出{bn}的前n项和,根据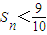 建立不等式,解之即可求出n的最值范围,即可求出所求.
建立不等式,解之即可求出n的最值范围,即可求出所求.解答:解:(I)由an=
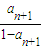 ⇒
⇒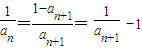 得
得 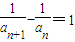
∴数列
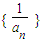 是首项为
是首项为 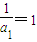 ,公差为1的等差数列
,公差为1的等差数列(II)由(I)知
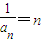 ,
,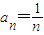 ∴
∴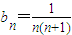 =
=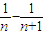
∴{bn}的前n项和为:
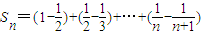 =1-
=1-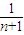
由题知1-
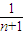 <
<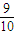 解得n<9所以n的最大值为8.
解得n<9所以n的最大值为8.点评:本题主要考查了等差数列的判定,以及利用裂项求和法进行求和,同时考查了不等式的解法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
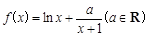 .
.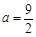 时,如果关于
时,如果关于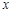 的方程:
的方程: 有且只有一个解,求实数
有且只有一个解,求实数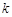 的取值范围;
的取值范围; 时,试比较
时,试比较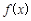 与1的大小;
与1的大小;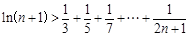
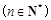 .
.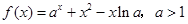 .
.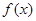 在
在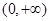 上单调递增;
上单调递增;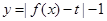 有三个零点,求
有三个零点,求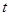 值;
值;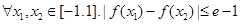 恒成立,求
恒成立,求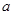 的取值范围.
的取值范围.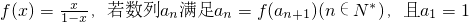 .
. 是等差数列;
是等差数列;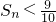 成立的n的最大值.
成立的n的最大值.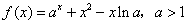 .
.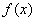 在
在 上单调递增;
上单调递增;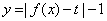 有三个零点,求
有三个零点,求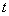 值;
值;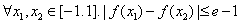 恒成立,求
恒成立,求 的取值范围.
的取值范围.