题目内容
已知函数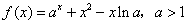 .
.
(I)求证: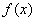 在
在 上单调递增;
上单调递增;
(Ⅱ)函数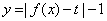 有三个零点,求
有三个零点,求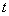 值;
值;
(Ⅲ)对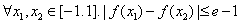 恒成立,求
恒成立,求 的取值范围.
的取值范围.
【答案】
解:(I) ,
,
由于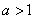 ,故尝
,故尝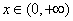 时,
时,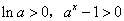 ,所以
,所以 ,
,
故函数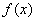 在
在 上单调递增。,
上单调递增。,
(Ⅱ)令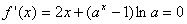 ,得到
,得到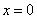 ,
,
因为函数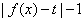 有三个零点,所以
有三个零点,所以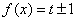 有三个根,
有三个根,
因为当 时,
时,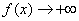 ,所以
,所以 ,故
,故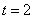
(Ⅲ)由(Ⅱ)可知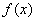 在区间
在区间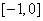 上单调递减,在区间
上单调递减,在区间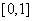 上单调递增。
上单调递增。
所以 ,
,
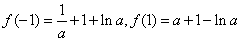
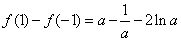
记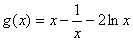
则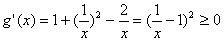 (仅在
(仅在 时取到等号),
时取到等号),
所以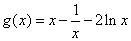 递增,故
递增,故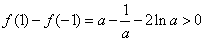 ,
,
所以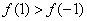 ,
于是
,
于是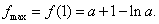
故对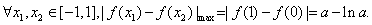
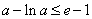 ,所以
,所以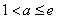 。
。

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 .
. 时,若函数
时,若函数 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围; ,
, ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线 的值.
的值. .
. .
. ,,求△ABC的面积.
,,求△ABC的面积. ,且
,且 .(I)求
.(I)求 的值;(II)求函数
的值;(II)求函数 在[1,3]上的最小值和最大值.
在[1,3]上的最小值和最大值.