题目内容
【题目】已知二次函数 f (x) = x 2 + x,若不等式 f (-x) + f (x)≤2 | x | 的解集为C. (1)求集合C (2)若方程 f (a x)-a x + 1 = 5(a > 0,a≠1)在 C上有解,求实数 a 的取值范围; (3)记 f (x) 在C 上的值域为 A,若 g(x) = x 3-3tx + ![]() ,x∈[0,1] 的值域为B,且 A B,求实数 t 的取值范围.
,x∈[0,1] 的值域为B,且 A B,求实数 t 的取值范围.
【答案】(1)[-1,1](2)0 < a≤![]() 或 a≥5(3)
或 a≥5(3)![]()
【解析】试题分析:(1)根据绝对值定义将不等式化为两个不等式组,分别求解,最后求并集(2)将方程转化为关于![]() 二次方程,根据底与1的大小分类讨论方程有解的条件,结合零点存在定理实数 a 的取值范围;(3)先利用导数研究函数g(x)单调性,确定其值域,再根据A B,利用数轴列条件,求实数 t 的取值范围.
二次方程,根据底与1的大小分类讨论方程有解的条件,结合零点存在定理实数 a 的取值范围;(3)先利用导数研究函数g(x)单调性,确定其值域,再根据A B,利用数轴列条件,求实数 t 的取值范围.
试题解析:解:(1) f (x) + f (-x) = 2x 2
当 x≥0时,2x 2≤2x 0≤x≤1
当 x < 0时, 2x 2≤-2x -1≤x < 0
∴集合 C = [-1,1]
(2) f (a x)-a x + 1-5 = 0 (a x) 2-(a-1)a x-5 = 0,令 a x = u
则方程为 h(u) = u 2-(a-1)u-5 = 0 h(0) = -5
当 a > 1时,u∈[![]() ,a],h(u) = 0 在 [
,a],h(u) = 0 在 [![]() ,a] 上有解,
,a] 上有解,
则 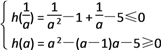 a≥5
a≥5
当 0 < a < 1时,u∈[a,![]() ],h(u) = 0 在 [a,
],h(u) = 0 在 [a,![]() ]上有解,
]上有解,
则 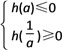 0 < a≤
0 < a≤![]()
∴当 0 < a≤![]() 或 a≥5时,方程在C上有解,且有唯一解。
或 a≥5时,方程在C上有解,且有唯一解。
(3) A = [-![]() ,2]
,2]
∵![]() ,∴
,∴ ![]() .
.
①当 t≤0时,函数 g(x) = x 3-3tx +![]() 在 x∈[0,1]单调递增,
在 x∈[0,1]单调递增,
∴函数 g(x)的值域 B =[![]() ,
,![]() ],
],
∵ A B ,∴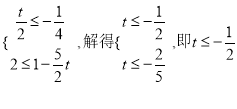 ,
,
②当t≥1时,令![]() ,得函数 g(x)的单调递减区间为:
,得函数 g(x)的单调递减区间为: ![]() ,
,
∵![]()
∴函数 g(x)在区间 [0,1]单调递减, B = [![]() ]
]
∴
![]()
③当 0 < t < 1 时,同理可得:
函数 g(x)的单调递减区间为: ![]() ;g(x)的单调递增区间为:[
;g(x)的单调递增区间为:[![]() ,1].
,1].
g(x)在 x =![]() 达到最小值。
达到最小值。
要使 A B,则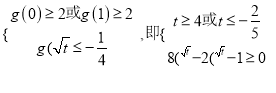
∵0 < t < 1,所以使得 A B的 t无解。
综上所述:t的取值范围是: ![]()

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案