题目内容
14.现有3本不同的数学书,4本不同的物理书,2本不同的化学书.(Ⅰ)若全部排在书架的同一层且不使同类的书分开,一共有多少种排法?
(Ⅱ)若从中任取5本书,求:
①恰有2本数学书,2本无理数,1本化学书,有多少种不同的取法?
②至少有1本数学书,有多少种不同的取法?
分析 (Ⅰ)根据题意,用捆绑法分析:先把3本不同的数学书“捆绑”在一起看成一本书,4本不同的物理书“捆绑”在一起看成一本书,2本不同的化学书“捆绑”在一起看成一本书,再分析3个元素之间的排法数目,由根据分步计数原理计算可得答案;
(Ⅱ)①根据题意,线分别计算“抽取2本数学书”、“抽取2本物理书”、“抽取1本化学书”的取法数目,再根据分步计数原理计算可得答案;
②根据题意,用排除法分析:先计算“在9本书中任取5本”的取法数目,再计算“没有数学书”的取法数目,由间接法计算可得答案.
解答 解:(Ⅰ)把3本不同的数学书“捆绑”在一起看成一本书,3本不同的数学书有A33种排法,
4本不同的物理书“捆绑”在一起看成一本书,4本不同的物理书有A44种排法,
2本不同的化学书“捆绑”在一起看成一本书,2本不同的化学书有A22种排法;
3个元素之间有A33种排法,
再根据分步计数原理,共有A33A44A22A33=1728种不同的排法.
(Ⅱ)①抽取2本数学书有C32=3种方法,
抽取2本物理书有C42=6种方法,
抽取1本化学书有C21=2种方法,
再根据分步计数原理,共有3×6×2=36种不同的取法,
②先不考虑书的不同,在9本书中任取5本,有C95种取法,
其中没有数学书,即在其他6本数中任取5本的取法有C65种,
间接法,共有C95-C65=120种取法.
点评 本题考查排列、组合的应用,涉及分类、分步计数原理的运用,解题时注意常见问题的处理方法,如用捆绑法处理必须相邻问题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
4.下列事件是随机事件的是( )
(1)连续两次掷一枚硬币,两次都出现正面向上.(2)异性电荷相互吸引
(3)在标准大气压下,水在1℃时结冰 (4)任意掷一枚骰子朝上的点数是偶数.
(1)连续两次掷一枚硬币,两次都出现正面向上.(2)异性电荷相互吸引
(3)在标准大气压下,水在1℃时结冰 (4)任意掷一枚骰子朝上的点数是偶数.
| A. | (1)(2) | B. | (2)(3) | C. | (3)(4) | D. | (1)(4) |
9.曲线y=$\frac{x}{x+2}$在点(-1,-1)处的切线方程为( )
| A. | y=-2x-3 | B. | y=x | C. | y=2x+1 | D. | y=-1 |
19.已知i是虚数单位,则1+i+i2…+i100等于( )
| A. | 1-i | B. | 1+i | C. | 0 | D. | 1 |
10.已知$sin(π+α)=\frac{{\sqrt{3}}}{2}$,则$cos(α-\frac{3π}{2})$的值是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
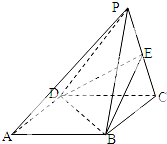 如图,四棱锥P-ABCD中,底面ABCD为矩形,PB=PC=AB,PB⊥平面PDC,E为棱PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PB=PC=AB,PB⊥平面PDC,E为棱PC的中点.