题目内容
10.数列{an}与{bn}满足:①a1=a<0,b1=b>0,②当k≥2时,若ak-1+bk-1≥0,则ak=ak-1,bk=$\frac{{a}_{k-1}+{b}_{k-1}}{2}$;若ak-1+bk-1<0,则ak=$\frac{{a}_{k-1}+{b}_{k-1}}{2}$,bk=bk-1.(Ⅰ)若a=-1,b=1,求a2,b2,a3,b3的值;
(Ⅱ)设Sn=(b1-a1)+(b2-a2)+…+(bn-an),求Sn(用a,b表示);
(Ⅲ)若存在n∈N*,对任意正整数k,当2≤k≤n时,恒有bk-1>bk,求n的最大值(用a,b表示).
分析 (Ⅰ)由题意可直接写出答案;
(Ⅱ)分情况计算bk-ak,得{bk-ak}是以b1-a1=b-a为首项,$\frac{1}{2}$为公比的等比数列,从而可得Sn;
(Ⅲ)由bk-1>bk,数列{an}与{bn}满足的关系倒推出对任意正整数k,当2≤k≤n时,恒有ak=a,结合(Ⅱ)知$a+a+(b-a)(\frac{1}{2})^{k-2}≥0$,解之即可.
解答 解:(Ⅰ)a2=-1,b2=0,a3=$-\frac{1}{2}$,b3=0;
(Ⅱ)∵$\frac{{a}_{k-1}+{b}_{k-1}}{2}-{a}_{k-1}$=$\frac{{b}_{k-1}-{a}_{k-1}}{2}$,${b}_{k-1}-\frac{{a}_{k-1}+{b}_{k-1}}{2}$=$\frac{{b}_{k-1}-{a}_{k-1}}{2}$,
∴无论是ak-1+bk-1≥0,还是ak-1+bk-1<0,都有bk-ak=$\frac{{b}_{k-1}-{a}_{k-1}}{2}$,
即{bk-ak}是以b1-a1=b-a为首项,$\frac{1}{2}$为公比的等比数列,
所以Sn=(b1-a1)+(b2-a2)+…+(bn-an)=$2(b-a)(1-\frac{1}{{2}^{n}})$;
(Ⅲ)∵bk-1>bk,及数列{an}与{bn}满足的关系,
∴ak-1+bk-1≥0,∴ak=ak-1,
即对任意正整数k,当2≤k≤n时,恒有ak=a,
由(Ⅱ)知bk-ak=$(b-a)(\frac{1}{2})^{k-1}$,∴bk=a+$(b-a)(\frac{1}{2})^{k-1}$,
所以ak-1+bk-1=$a+a+(b-a)(\frac{1}{2})^{k-2}≥0$,解得$k≤2+lo{g}_{\frac{1}{2}}\frac{-2a}{b-a}$,
所以n的最大值为不超过$2+lo{g}_{\frac{1}{2}}\frac{-2a}{b-a}$的最大整数.
点评 本题考查数列中递推关系,以及解指数不等式,考查学生对数学知识的应用能力,属于中档题.

| 4S店的小型汽车维修保养 | 公共wifi的安全性 | 网络购物 | |
| 满意 | 200人 | 400人 | 800人 |
| 不满意 | 400人 | 100人 | 400人 |
(Ⅱ)在对参与网络购物满意度调查的人员中,用分层抽样的方法抽取6人,再从这6人中任意选取2人,求恰有1人对网络购物满意的概率.
| A. | -1 | B. | 0 | C. | 1 | D. | i |
| A. | {x|-1≤x<2} | B. | {x|-2≤x<4} | C. | {x|-1<x<4} | D. | {x|-4<x≤4} |
| A. | -5+12i | B. | -5-12i | C. | -13+12i | D. | -13-12i |
 如图是某中学参加高三体育考试的学生中抽取60名学生的体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图中的信息回答下列问题:
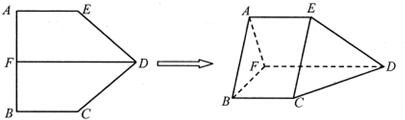
如图是某中学参加高三体育考试的学生中抽取60名学生的体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图中的信息回答下列问题: 如图,在五面体ABCDEF中,四边形 ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.
如图,在五面体ABCDEF中,四边形 ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.