题目内容
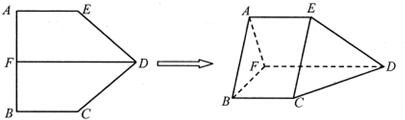
5.如图,在五边形ABCDE中,AB⊥BC,AE∥BC∥FD,F为AB的中点,AB=FD=2BC=2AE,现把此五边形ABCDE沿FD折成一个60°的二面角.
(Ⅰ)求证:直线CE∥平面ABF;
(Ⅱ)求二面角E-CD-F的平面角的余弦值.
分析 (Ⅰ)先证明四边形ABCE为平行四边形得到CE∥AB,从而直线CE∥平面ABF;
(Ⅱ)取FD得中点G,如图作辅助线.先证明DF⊥平面ABF,从而DF⊥平面ECG,所以DF⊥EH,又EH⊥CD,所以EH⊥CD,又HI⊥CD,所以CD⊥平面EHI,从而CD⊥EI,从而∠EIH为二面角E-CD-F的平面角.代入数据计算即可.
解答 (Ⅰ)证明:∵AE∥DF,BC∥FD,∴AE∥BC,
又∵BC=AE,∴四边形ABCE为平行四边形,∴CE∥AB.
又CE?平面ABF,AB?平面ABF,所以直线CE∥平面ABF;
(Ⅱ)解:如图,取FD得中点G,连接EG、CG,
在△CEG中,作EH⊥CG,垂足为H,
在平面BCDF中,作HI⊥CD,垂足为I,连接EI.
∵AE=FG=BC,AE∥FG∥BC,∴AF∥EG,BF∥CG.
又DF⊥AF,DF⊥BF,故DF⊥平面ABF,所以DF⊥平面ECG,
∵EH⊥CG,DF⊥EH,∴EH⊥平面CGD,∴EH⊥CD,
又∵HI⊥CD,∴CD⊥平面EHI,所以CD⊥EI,
从而∠EIH为二面角E-CD-F的平面角.
设BC=AE=1,则FG=GD=CG=GE=1,
由于∠EGC为二面角C-FD-E的平面角,即∠EGC=60°,
所以在△CEG中,HG=CH=$\frac{1}{2}$,EH=$\frac{\sqrt{3}}{2}$,HI=CHsin45°=$\frac{\sqrt{2}}{4}$,
所以EI=$\frac{\sqrt{14}}{4}$,所以cos∠EIH=$\frac{\sqrt{7}}{7}$.
点评 本题考查空间角、空间中直线与平面的位置关系,属中档题.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
20.某书店订购一本新版图书,根据以往经验预测,这本新书的预售量为40,100,120(本)的概率分别为0.2,0.7,0.1,这本书的订购价为6元,销售价为8元,如果售不出去,以每本为5元的价格处理书,试用盈利决定书店应订购多少本新书?
| 自然状况 | 概率\盈利(元)\方案 | 订购40本 | 订购100本 | 订购120本 |
| 销售40本 | 0.2 | |||
| 销售100本 | 0.7 | |||
| 销售120本 | 0.1 |
14. 某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )
某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )
 某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )
某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{8}{3}$ |
 已知矩形ABCD中,AB=1,BC=$\sqrt{3}$,将此矩形按如图所示流程沿地面上一直线滚动,在滚动过程中,始终与地面垂直,设BC与地面所成角为θ,矩形周边上最高点离地面的距离为f(θ),求:
已知矩形ABCD中,AB=1,BC=$\sqrt{3}$,将此矩形按如图所示流程沿地面上一直线滚动,在滚动过程中,始终与地面垂直,设BC与地面所成角为θ,矩形周边上最高点离地面的距离为f(θ),求: 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为$\frac{1}{2}$.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为$\frac{1}{2}$.