题目内容
已知函数f(x)= 若|f(x)|≥ax,则a的取值范围是________.
若|f(x)|≥ax,则a的取值范围是________.
 若|f(x)|≥ax,则a的取值范围是________.
若|f(x)|≥ax,则a的取值范围是________.[-2,0]
当x≤0时,f(x)=-x2+2x=-(x-1)2+1≤0,所以|f(x)|≥ax,化简为x2-2x≥ax,即x2≥(a+2)x,因为x≤0,所以a+2≥x恒成立,所以a≥-2;当x>0时,f(x)=ln(x+1)>0,所以|f(x)|≥ax化简为ln(x+1)>ax恒成立,由函数图象可知a≤0,综上,当-2≤a≤0时,不等式|f(x)|≥ax恒成立.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 米,圆心角为
米,圆心角为 (弧度).
(弧度).
 关于
关于 ,求
,求 的函数关系式,并求出
的函数关系式,并求出 x+
x+ x=1的解”有如下解题思路:设f(x)=
x=1的解”有如下解题思路:设f(x)=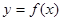 的周期为2,当
的周期为2,当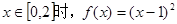 ,如果
,如果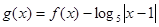 ,则函数
,则函数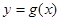 的所有零点之和为( )
的所有零点之和为( ) +
+ 的最小值为________.
的最小值为________. ,若数列
,若数列 满足
满足 ,则
,则




 ,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|.
,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|.