题目内容
已知点G是△ABC的重心,A(0,-1),B(0,1).在x轴上有一点M,满足|(1)求点C的轨迹E的方程;
(2)设(1)中曲线E的左、右焦点分别为F1、F2,过点F2的直线l交曲线E于P、Q两点,求△F1PQ面积的最大值,并求出取最大值时直线l的方程.
解:(1)设C(x,y),则G(![]() ,
,![]() ).
).
∵![]() =λ
=λ![]() (λ∈R),∴GM∥AB.又M是x轴上一点,则M(
(λ∈R),∴GM∥AB.又M是x轴上一点,则M(![]() ,0),
,0),
又∵|![]() |=|
|=|![]() |,∴(
|,∴(![]() =
=![]() .整理得
.整理得![]() +y2=1(x≠0).
+y2=1(x≠0).
(2)由(1),知F1(-![]() ,0),F2(
,0),F2(![]() ,0).
,0).
设直线l的方程为x=ty+![]() ,由(1),知x≠0,∴l不过点(0,±1).∴t≠±
,由(1),知x≠0,∴l不过点(0,±1).∴t≠±![]() .
.
设P(x1,y1),Q(x2,y2),将x=ty+![]() 代入x2+3y2=3,(t2+3)y2+2
代入x2+3y2=3,(t2+3)y2+2![]() ty-1=0.∴Δ=8t2+4(t2+3)=12(t2+1)>0恒成立.∴y1+y2=
ty-1=0.∴Δ=8t2+4(t2+3)=12(t2+1)>0恒成立.∴y1+y2=![]() ,y1·y2=
,y1·y2=![]() .
.
∴|y1-y2|=![]() =
=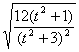 =
=![]() .
.
∴![]() =
=![]() |F1F2|·|y1-y2|=
|F1F2|·|y1-y2|=![]() |y1-y2|=2
|y1-y2|=2![]()
![]() (t≠±
(t≠±![]() ).
).
∴![]() =
=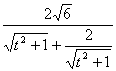 ≤
≤![]() =
=![]() .
.
当且仅当t2+1=2,即t=±1时取“=”.
∴△F1PQ的最大值为3,此时直线l的方程为x±y-2=0.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知点G是△ABC的重心,点P是△GBC内一点,若
=λ
+μ
,则λ+μ的取值范围是( )
| AP |
| AB |
| AC |
A、(
| ||
B、(
| ||
C、(1,
| ||
| D、(1,2) |