题目内容
(文)已知奇函数f(x)满足f(x+3)=f(x),当x∈(0,1)时,函数f(x)=3x-1,则f(log| 1 |
| 3 |
(理)已知点G是△ABC的重心,O是空间任意一点,若
| OA |
| OB |
| OC |
| OG |
分析:(文)由函数是奇函数得到f(-x)=-f(x)和f(x+3)=f(x)把则f( log
36)进行变形得到 log3
∈(0,1)时函数f(x)=3x-1,求出即可.
(理)本题中的所给的向量等式不易处理,考虑到点G是△ABC的重心,故可根据重心的性质先得到相关的向量方程,再由向量的运算规则将等式中的向量用题设中的四个向量表示出来,整理,根据同一性求得参数的值.
| 1 |
| 3 |
| 36 |
| 27 |
(理)本题中的所给的向量等式不易处理,考虑到点G是△ABC的重心,故可根据重心的性质先得到相关的向量方程,再由向量的运算规则将等式中的向量用题设中的四个向量表示出来,整理,根据同一性求得参数的值.
解答:(文)解:函数f(x)满足f(x+3)=f(x)和f(-x)=-f(x)
则f( log
36)=f(-log336)=-f(log336)=-f(log336-3)=-f(log3
),
因为 log3
∈(0,1)
则f(log
36)=-(3 log 3
-1)=-
故答案为-
;
(理)解:由于G是三角形ABC的重心,则有
+
+
=
,
-
+
-
+
-
=
故
+
+
=3
又由已知
+
+
=λ
故可得λ=3
故答案为:3
则f( log
| 1 |
| 3 |
| 36 |
| 27 |
因为 log3
| 36 |
| 27 |
则f(log
| 1 |
| 3 |
| 36 |
| 27 |
| 1 |
| 3 |
故答案为-
| 1 |
| 3 |
(理)解:由于G是三角形ABC的重心,则有
| GA |
| GB |
| GC |
| 0 |
| OA |
| OG |
| OB |
| OG |
| OC |
| OG |
| 0 |
故
| OA |
| OB |
| OC |
| OG |
又由已知
| OA |
| OB |
| OC |
| OG |
故可得λ=3
故答案为:3
点评:(文)考查学生应用函数奇偶性的能力,函数的周期性的掌握能力,以及运用对数的运算性质能力.
(理)本题考查向量的相等及向量的加减运算法则,向量数乘的概念,三角形重心的几何性质,是向量在几何中应用的基本题型.解决本题的关键是利用重心的几何性质建立起向量等式,此类题一定要注意找准下手的角度.
(理)本题考查向量的相等及向量的加减运算法则,向量数乘的概念,三角形重心的几何性质,是向量在几何中应用的基本题型.解决本题的关键是利用重心的几何性质建立起向量等式,此类题一定要注意找准下手的角度.

练习册系列答案
相关题目
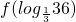 =________
=________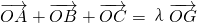 ,则λ的值是________.
,则λ的值是________.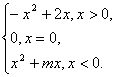
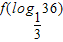 =
= 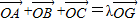 ,则λ的值是 .
,则λ的值是 .