题目内容
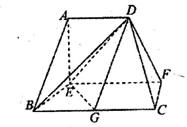
在如图所示的多面体中,底面BCFE是梯形,EF//BC,又EF 平面AEB,AE
平面AEB,AE EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.
EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.
(1)求证:AB//平面DEG;
(2)求证:BD EG;
EG;
(3)求二面角C—DF—E的正弦值.
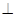 平面AEB,AE
平面AEB,AE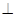 EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.
EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.(1)求证:AB//平面DEG;
(2)求证:BD
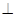 EG;
EG;(3)求二面角C—DF—E的正弦值.

(1)见解析;(2)见解析;(3)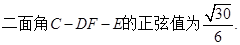
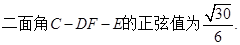
试题分析:(1)利用已有平行关系,可得到
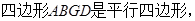 得到
得到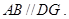 而得证.
而得证.(2)通过证明
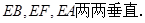 以点
以点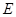 为坐标原点,
为坐标原点,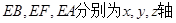 ,建立空间直角坐标系,根据
,建立空间直角坐标系,根据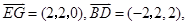 计算它们的数量积为零,得证.
计算它们的数量积为零,得证.(3)由已知可得
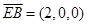 是平面
是平面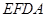 的一个法向量.
的一个法向量.确定平面
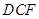 的一个法向量为
的一个法向量为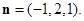
利用
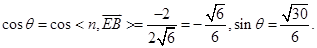 得解.
得解.(1)证明:
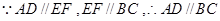 ,
,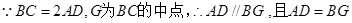 .
.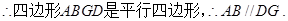 2分
2分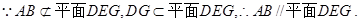 4分
4分(2)证明:
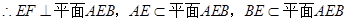 ,
,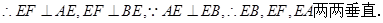 6分
6分以点
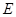 为坐标原点,
为坐标原点,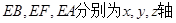 ,建立空间直角坐标系如图所示,由已知得
,建立空间直角坐标系如图所示,由已知得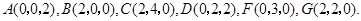
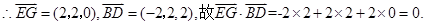
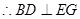 8分
8分(3)由已知可得
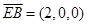 是平面
是平面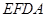 的一个法向量.
的一个法向量.设平面
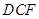 的一个法向量为
的一个法向量为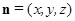 ,
,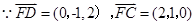 ,
,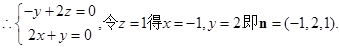 10分
10分设二面角
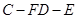 的大小为
的大小为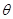 ,
,则
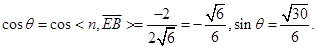 11分
11分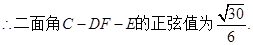 12分
12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的所有棱长都相等,
的所有棱长都相等, ,四边形
,四边形 和四边形
和四边形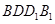 为矩形.
为矩形. 底面
底面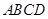 ;
; ,求二面角
,求二面角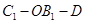 的余弦值.
的余弦值.
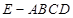 中,平面
中,平面
 平面
平面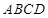 ,
,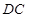 //
//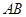 ,
,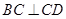 ,
,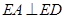 ,且
,且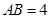 ,
,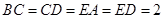 .
.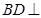 平面
平面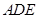 ;
;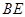 和平面
和平面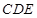 所成角的正弦值;
所成角的正弦值; 上是否存在一点
上是否存在一点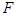 使得平面
使得平面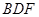
 平面
平面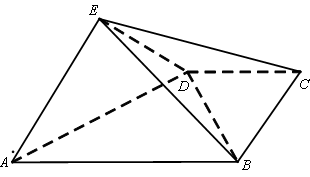
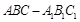 中,
中,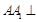 底面
底面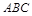 ,
,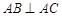 ,
,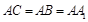 ,
,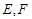 分别是棱
分别是棱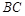 ,
,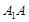 的中点,
的中点,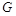 为棱
为棱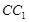 上的一点,且
上的一点,且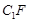 //平面
//平面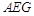 .
.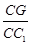 的值;
的值;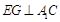 ;
; 的余弦值.
的余弦值.
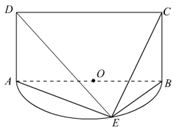
 是以
是以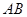 为直径的半圆
为直径的半圆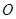 上异于
上异于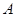 、
、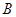 的点,矩形
的点,矩形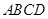 所在的平面垂直于半圆
所在的平面垂直于半圆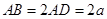 .
.
 ;
; 和
和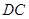 所成的角为
所成的角为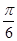 ,求平面
,求平面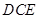 与平面
与平面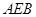 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.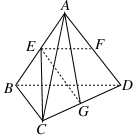
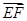 ·
·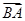 ;
;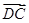 ;
;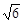 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记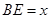 ,用
,用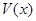 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.
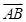 ,
,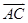 为边的平行四边形的面积;
为边的平行四边形的面积;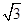 ,且a分别与
,且a分别与