Question

已知实数x，y满足：

x-y+2≥0 y≥ 1 2 x+1 x+y-1≥0

，则目标函数z=2x-y（　　）

• A．有最大值4
• B．有最小值-4
• C．有最小值-

  5

  2

• D．既无最大值也无最小值

Answer 1

分析：确定可行域，明确目标函数的几何意义：直线y=2x-z的纵截距的相反数，即可得到结论．

解答：解：不等式对应的区域如图：

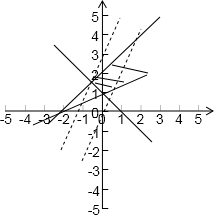
目标函数z=2x-y的几何意义是直线y=2x-z的纵截距的相反数
由

x+y-1=0 x-y+2=0

可得

x=- 1 2 y= 3 2

，从而可得在（-

1

2

，

3

2

）处直线y=2x-z的纵截距最大，则z最小为-

5

2

；z无最大值．
故选C．

点评：本题考查线性规划知识，考查学生的计算能力，解题的关键是确定可行域，明确目标函数的几何意义．